One of the filter structures introduced in Book II [452, p.
209] was the parallel second-order filter bank, which
may be computed from the general transfer function (a ratio of
polynomials in ![]() ) by means of the Partial Fraction Expansion
(PFE) [452, p. 129]:
) by means of the Partial Fraction Expansion
(PFE) [452, p. 129]:
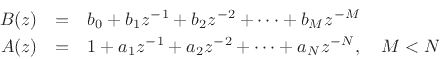
The PFE Eq.(1.12) expands the (strictly proper2.10) transfer function as a
parallel bank of (complex) first-order resonators. When the
polynomial coefficients ![]() and
and ![]() are real, complex poles
are real, complex poles ![]() and
residues
and
residues ![]() occur in conjugate pairs, and these can be
combined to form second-order sections [452, p. 131]:
occur in conjugate pairs, and these can be
combined to form second-order sections [452, p. 131]:
![\begin{eqnarray*}
H_i(z) &\!=\!& \frac{r_i}{1-p_iz^{-1}} + \frac{\overline{r_i}}{1-\overline{p_i}z^{-1}} \eqsp
\frac{r_i-r_i\overline{p_i}z^{-1}+\overline{r_i}-\overline{r_i} p_iz^{-1}}{(1-p_iz^{-1})(1-\overline{p_i}z^{-1})}\\ [5pt]
&\!=\!&
\frac{2\mbox{re}\left\{r_i\right\}-2\mbox{re}\left\{r_i\overline{p_i}\right\}z^{-1}}{1-2\mbox{re}\left\{p_i\right\}z^{-1}+ \left\vert p_i\right\vert^2 z^{-2}}
\eqsp 2G_i\frac{\cos(\phi_i)-\cos(\phi_i-\theta_i)z^{-1}}{1-2R_i\,\cos(\theta_i)z^{-1}+ R_i^2 z^{-2}}.
\end{eqnarray*}](img304.png)
where
![]() and
and
![]() . Thus, every transfer function
. Thus, every transfer function ![]() with real
coefficients can be realized as a parallel bank of real first- and/or
second-order digital filter sections, as well as a parallel FIR branch
when
with real
coefficients can be realized as a parallel bank of real first- and/or
second-order digital filter sections, as well as a parallel FIR branch
when ![]() .
.
As we will develop in §8.5, modal synthesis employs a ``source-filter'' synthesis model consisting of some driving signal into a parallel filter bank in which each filter section implements the transfer function of some resonant mode in the physical system. Normally each section is second-order, but it is sometimes convenient to use larger-order sections; for example, fourth-order sections have been used to model piano partials in order to have beating and two-stage-decay effects built into each partial individually [30,29].
For example, if the physical system were a row of tuning forks (which are designed to have only one significant resonant frequency), each tuning fork would be represented by a single (real) second-order filter section in the sum. In a modal vibrating string model, each second-order filter implements one ``ringing partial overtone'' in response to an excitation such as a finger-pluck or piano-hammer-strike.