Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Note that a general 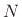 th-order state-space model Eq.(1.8) requires
around
th-order state-space model Eq.(1.8) requires
around 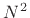 multiply-adds to update for each time step (assuming the
number of inputs and outputs is small compared with the number of
state variables, in which case the
multiply-adds to update for each time step (assuming the
number of inputs and outputs is small compared with the number of
state variables, in which case the
 computation dominates).
After diagonalization by a similarity transform, the time update is
only order
computation dominates).
After diagonalization by a similarity transform, the time update is
only order 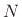 , just like any other efficient digital filter
realization. Thus, a diagonalized state-space model (modal
representation) is a strong contender for applications in which
it is desirable to have independent control of resonant modes.
, just like any other efficient digital filter
realization. Thus, a diagonalized state-space model (modal
representation) is a strong contender for applications in which
it is desirable to have independent control of resonant modes.
Another advantage of the modal expansion is that frequency-dependent
characteristics of hearing can be brought to bear. Low-frequency
resonances can easily be modeled more carefully and in more detail
than very high-frequency resonances which tend to be heard only
``statistically'' by the ear. For example, rows of high-frequency
modes can be collapsed into more efficient digital waveguide loops
(§8.5) by retuning them to the nearest harmonic mode series.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() th-order state-space model Eq.(1.8) requires
around
th-order state-space model Eq.(1.8) requires
around ![]() multiply-adds to update for each time step (assuming the
number of inputs and outputs is small compared with the number of
state variables, in which case the
multiply-adds to update for each time step (assuming the
number of inputs and outputs is small compared with the number of
state variables, in which case the
![]() computation dominates).
After diagonalization by a similarity transform, the time update is
only order
computation dominates).
After diagonalization by a similarity transform, the time update is
only order ![]() , just like any other efficient digital filter
realization. Thus, a diagonalized state-space model (modal
representation) is a strong contender for applications in which
it is desirable to have independent control of resonant modes.
, just like any other efficient digital filter
realization. Thus, a diagonalized state-space model (modal
representation) is a strong contender for applications in which
it is desirable to have independent control of resonant modes.