Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
To diagonalize our force-driven mass example, we may begin with its
state-space model Eq.(1.9):
which is in the general state-space form
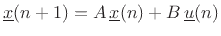 as needed (Eq.(1.8)). We can see that
as needed (Eq.(1.8)). We can see that 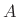 is already a
Jordan block of order 2 [452, p. 368]. (We can change the
is already a
Jordan block of order 2 [452, p. 368]. (We can change the
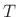 to 1 by scaling the physical units of
to 1 by scaling the physical units of 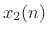 .) Thus, the system
is already as diagonal as it's going to get. We have a repeated pole
at
.) Thus, the system
is already as diagonal as it's going to get. We have a repeated pole
at  , and they are effectively in series (instead of parallel),
thus giving a ``defective''
, and they are effectively in series (instead of parallel),
thus giving a ``defective'' 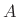 matrix [452, p. 136].
matrix [452, p. 136].
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![$\displaystyle \left[\begin{array}{c} x_{n+1} \\ [2pt] v_{n+1} \end{array}\right]
\eqsp \left[\begin{array}{cc} 1 & T \\ [2pt] 0 & 1 \end{array}\right]\left[\begin{array}{c} x_n \\ [2pt] v_n \end{array}\right]
+ \left[\begin{array}{c} 0 \\ [2pt] T/m \end{array}\right] f_n, \quad n=0,1,2,\ldots
$](img308.png)
![$\displaystyle \left[\begin{array}{c} x_{n+1} \\ [2pt] v_{n+1} \end{array}\right]
\eqsp \left[\begin{array}{cc} 1 & T \\ [2pt] 0 & 1 \end{array}\right]\left[\begin{array}{c} x_n \\ [2pt] v_n \end{array}\right]
+ \left[\begin{array}{c} 0 \\ [2pt] T/m \end{array}\right] f_n, \quad n=0,1,2,\ldots
$](img308.png)