This section (adapted from [432]), summarizes some of the more commonly used methods for digital filter design aimed at matching a nonparametric frequency response, such as typically obtained from input/output measurements. This problem should be distinguished from more classical problems with their own specialized methods, such as designing lowpass, highpass, and bandpass filters [346,365], or peak/shelf equalizers [563,452], and other utility filters designed from a priori mathematical specifications.
The problem of fitting a digital filter to a prescribed frequency
response may be formulated as follows. To simplify, we set ![]() .
.
Given a continuous complex function
![]() ,
corresponding to a causal desired frequency response,9.8 find a stable digital filter of the form
,
corresponding to a causal desired frequency response,9.8 find a stable digital filter of the form
where
| (9.15) | |||
| (9.16) |
with
![]() given, such that some norm of the error
given, such that some norm of the error
![$\displaystyle \hat{\theta}^K\isdefs [{\hat b}_0,{\hat b}_1,\ldots\,,{\hat b}_{\hat{N}_b},{\hat a}_1,{\hat a}_2,\ldots\,,{\hat a}_{\hat{N}_a}].
$](img1842.png)
The filter coefficients are constrained to lie in some subset
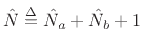 . The filter
coefficients may also be complex, in which case
. The filter
coefficients may also be complex, in which case
The approximate filter ![]() is typically constrained to be
stable, and since
is typically constrained to be
stable, and since
![]() is causal (no positive powers of
is causal (no positive powers of ![]() ),
stability implies causality. Consequently, the impulse response of the
model
),
stability implies causality. Consequently, the impulse response of the
model
![]() is zero for
is zero for ![]() .
.
The filter-design problem is then to find a (strictly) stable
![]() -pole,
-pole,
![]() -zero digital filter which minimizes some norm of
the error in the frequency-response. This is fundamentally
rational approximation of a complex function of a real
(frequency) variable, with constraints on the poles.
-zero digital filter which minimizes some norm of
the error in the frequency-response. This is fundamentally
rational approximation of a complex function of a real
(frequency) variable, with constraints on the poles.
While the filter-design problem has been formulated quite naturally,
it is difficult to solve in practice. The strict stability assumption
yields a compact space of filter coefficients
![]() , leading to the
conclusion that a best approximation
, leading to the
conclusion that a best approximation
![]() exists over this
domain.9.9Unfortunately, the norm of the error
exists over this
domain.9.9Unfortunately, the norm of the error
![]() typically is
not a convex9.10function of the filter coefficients on
typically is
not a convex9.10function of the filter coefficients on
![]() . This
means that algorithms based on gradient descent may fail to find an
optimum filter due to their premature termination at a suboptimal
local minimum of
. This
means that algorithms based on gradient descent may fail to find an
optimum filter due to their premature termination at a suboptimal
local minimum of
![]() .
.
Fortunately, there is at least one norm whose global minimization may be accomplished in a straightforward fashion without need for initial guesses or ad hoc modifications of the complex (phase-sensitive) IIR filter-design problem--the Hankel norm [156,432,178,36]. Hankel norm methods for digital filter design deliver a spontaneously stable filter of any desired order without imposing coefficient constraints in the algorithm.
An alternative to Hankel-norm approximation is to reformulate the problem, replacing Eq.(8.17) with a modified error criterion so that the resulting problem can be solved by linear least-squares or convex optimization techniques. Examples include
![$\displaystyle \left\Vert\,{\hat A}(\ejo)H(\ejo)-{\hat B}(\ejo)\,\right\Vert
\eqsp \left\Vert\,{\hat A}(\ejo)\left[ H(\ejo)-{\hat H}(\ejo)\right]\,\right\Vert.
$](img1865.png)
When the
The above expression makes it clear that equation-error can be
seen as a frequency-response error weighted by
![]() . Thus, relatively large errors can be
expected where the poles of the optimum approximation (roots
of
. Thus, relatively large errors can be
expected where the poles of the optimum approximation (roots
of
![]() ) approach the unit circle
) approach the unit circle ![]() . While this may
make the frequency-domain formulation seem ill-posed, in the
time-domain, linear prediction error is minimized in
the
. While this may
make the frequency-domain formulation seem ill-posed, in the
time-domain, linear prediction error is minimized in
the
![]() sense, and in certain applications this is ideal.
(Equation-error methods thus provide a natural extension of
ratio-error methods to include zeros.) Using so-called
Steiglitz-McBride iterations
[289,452,290], the
equation-error solution iteratively approaches the
norm-minimizing solution of Eq.(8.17) for the
sense, and in certain applications this is ideal.
(Equation-error methods thus provide a natural extension of
ratio-error methods to include zeros.) Using so-called
Steiglitz-McBride iterations
[289,452,290], the
equation-error solution iteratively approaches the
norm-minimizing solution of Eq.(8.17) for the ![]() norm.
norm.
Examples of minimizing equation error using the matlab function invfreqz are given in §8.6.3 and §8.6.4 below. See [452, Appendix I] (based on [432, pp. 48-50]) for a discussion of equation-error IIR filter design and a derivation of a fast equation-error method based on the Fast Fourier Transform (FFT) (used in invfreqz).
In addition to these modifications, sometimes it is necessary to
reformulate the problem in order to achieve a different goal. For
example, in some audio applications, it is desirable to minimize the
log-magnitude frequency-response error. This is due to the way
we hear spectral distortions in many circumstances. A technique which
accomplishes this objective to the first order in the
![]() norm is
described in [432].
norm is
described in [432].
Sometimes the most important spectral structure is confined to an interval of the frequency domain. A question arises as to how this structure can be accurately modeled while obtaining a cruder fit elsewhere. The usual technique is a weighting function versus frequency. An alternative, however, is to frequency-warp the problem using a first-order conformal map. It turns out a first-order conformal map can be made to approximate very well frequency-resolution scales of human hearing such as the Bark scale or ERB scale [461]. Frequency-warping is especially valuable for providing an effective weighting-function for filter-design methods, such as the Hankel-norm method, which have no mechanism for imposing an explicit weighting-function on the frequency-response error.
There are several methods which produce
![]() instead of
instead of
![]() directly. A fast spectral factorization technique is
useful in conjunction with methods of this category [432].
Roughly speaking, a size
directly. A fast spectral factorization technique is
useful in conjunction with methods of this category [432].
Roughly speaking, a size
![]() polynomial factorization is replaced
by an FFT and a size
polynomial factorization is replaced
by an FFT and a size
![]() system of linear equations.
system of linear equations.