Ideal Differentiator (Spring Admittance)

Figure 8.1 shows a graph of the frequency response of the ideal differentiator (spring admittance). In principle, a digital differentiator is a filter whose frequency response $H(e^{j\omega T})$ optimally approximates $j\omega$ for $\omega T$ between $-\pi$ and $\pi$ . Similarly, a digital integrator must match $1/j\omega$ along the unit circle in the $z$ plane. The reason an exact match is not possible is that the ideal frequency responses $j\omega$ and $1/j\omega$ , when wrapped along the unit circle in the $z$ plane, are not ``smooth'' functions any more (see Fig.8.1). As a result, there is no filter with a rational transfer function (i.e., finite order) that can match the desired frequency response exactly.

Figure 8.1: Imaginary part of the frequency response $H(e^{j\omega T})=j\omega$ of the ideal digital differentiator plotted over the unit circle in the $z$ plane (the real part being zero).

The discontinuity at $z=-1$ alone is enough to ensure that no finite-order digital transfer function exists with the desired frequency response. As with bandlimited interpolation (§4.4), it is good practice to reserve a ``guard band'' between the highest needed frequency $f_{\mbox{\tiny max}}$ (such as the limit of human hearing) and half the sampling rate $f_s/2$ . In the guard band $[f_{\mbox{\tiny max}},f_s/2]$ , digital filters are free to smoothly vary in whatever way gives the best performance across frequencies in the audible band $[0,f_{\mbox{\tiny max}}]$ at the lowest cost. Figure 8.2 shows an example. Note that, as with filters used for bandlimited interpolation, a small increment in oversampling factor yields a much larger decrease in filter cost (when the sampling rate is near $2f_{\mbox{\tiny max}}$ ).

In the general case of Eq.(8.14) with $s=j\omega$ , digital filters can be designed to implement arbitrarily accurate admittance transfer functions by finding an optimal rational approximation to the complex function of a single real variable $\omega$

$$H(e^{j\omega}) \eqsp \frac{B(j\omega)}{A(j\omega)} \eqsp \frac{b_M (j\omega)^M + \cdots b_1 j\omega + b_0}{a_N (j\omega)^N + \cdots a_1 j\omega + a_0}$$

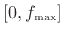
over the interval $-\omega_{\mbox{\tiny max}}\leq \omega \leq \omega_{\mbox{\tiny max}}$ , where $\omega_{\mbox{\tiny max}}T<\pi$ is the upper limit of human hearing. For small guard bands $\delta\isdeftext \pi-\omega_{\mbox{\tiny max}}T$ , the filter order required for a given error tolerance is approximately inversely proportional to $\delta$ .