Gradient Descent

Concavity is valuable in connection with the Gradient Method of minimizing $J({\hat \theta})$ with respect to ${\hat \theta}$.

Definition. The gradient of the error measure $J({\hat \theta})$ is defined as the ${\hat N}\times 1$ column vector

$${J^\prime}({\hat \theta})\mathrel{\stackrel{\mathrm{\Delta}}{=}}\... ...ial}{\partial \theta}{J(\theta)}{a_{n_a}}\left({\hat a}_{n_a}\right)\right]^T.$$

Definition. The Gradient Method (Cauchy) is defined as follows.

Given ${\hat \theta}_0\in{\hat \Theta}$, compute

$${\hat \theta}_{n+1} = {\hat \theta}_n - t_n {J^\prime}({\hat \theta}_n),\qquad n=1,2,\ldots\,,$$

where ${J^\prime}({\hat \theta}_n)$ is the gradient of $J$ at ${\hat \theta}_n$, and $t_n\in\Re$ is chosen as the smallest nonnegative local minimizer of

$$\Phi_n(t) \mathrel{\stackrel{\mathrm{\Delta}}{=}}J\left({\hat \theta}_n-t{J^\prime}({\hat \theta}_n)\right).$$

Cauchy originally proposed to find the value of $t_n\geq 0$ which gave a global minimum of $\Phi_n(t)$. This, however, is not always feasible in practice.

Some general results regarding the Gradient Method are given below.

Theorem. If ${\hat \theta}_0$ is a local minimizer of $J({\hat \theta})$, and ${J^\prime}({\hat \theta}_0)$ exists, then ${J^\prime}({\hat \theta}_0)=0$.

Theorem. The gradient method is a descent method, i.e., $J({\hat \theta}_{n+1})\leq J({\hat \theta}_n)$.

Definition. $J:{\hat \Theta}\rightarrow \Re ^1$, ${\hat \Theta}\subset\Re ^{\hat N}$, is said to be in the class ${\cal C}_k({\hat \Theta})$ if all $k$th order partial derivatives of $J({\hat \theta})$ with respect to the components of ${\hat \theta}$ are continuous on ${\hat \Theta}$.

Definition. The Hessian ${J^{\prime\prime}}({\hat \theta})$ of $J$ at ${\hat \theta}$ is defined as the matrix of second-order partial derivatives,

$${J^{\prime\prime}}({\hat \theta}) [i,j] \mathrel{\stackrel{\mathr... ...c{\partial^2 J(\theta)}{\partial \theta[i]\partial \theta[j]} ({\hat \theta}),$$

where $\theta[i]$ denotes the $i$th component of $\theta$, $i=1,\ldots\,,{\hat N}={n_a}+{n_b}+1$, and $[i,j]$ denotes the matrix entry at the $i$th row and $j$th column.

The Hessian of every element of ${\cal C}_2({\hat \Theta})$ is a symmetric matrix [7]. This is because continuous second-order partials satisfy

$$\frac{\partial^2}{\partial x_1\partial x_2} = \frac{\partial^2}{\partial x_2\partial x_1} .$$

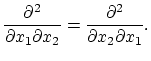
Theorem. If $J\in {\cal C}_1({\hat \Theta})$, then any cluster point ${\hat \theta}_\infty$ of the gradient sequence ${\hat \theta}_n$ is necessarily a stationary point, i.e., ${J^\prime}({\hat \theta}_\infty)=0$.

Theorem. Let $\overline{{\hat \Theta}}$ denote the concave hull of ${\hat \Theta}\subset\Re ^{\hat N}$. If $J\in {\cal C}_2({\hat \Theta})$, and there exist positive constants $c$ and $C$ such that

$$c\left\Vert\,\eta\,\right\Vert^2\leq \eta^T {J^{\prime\prime}}({\hat \theta}) \eta \leq C\left\Vert\,\eta\,\right\Vert^2,$$ (4)

for all ${\hat \theta}\in{\hat \Theta}$ and for all $\eta\in\Re ^{{\hat N}}$, then the gradient method beginning with any point in ${\hat \Theta}$ converges to a point ${\hat \theta}^\ast$. Moreover, ${\hat \theta}^\ast$ is the unique global minimizer of $J$ in $\Re ^{{\hat N}}$.

By the norm equivalence theorem [4], Eq. (4) is satisfied whenever ${J^{\prime\prime}}({\hat \theta})$ is a norm on ${\hat \Theta}$ for each ${\hat \theta}\in{\hat \Theta}$. Since ${J^{\prime\prime}}$ belongs to ${\cal C}_2({\hat \Theta})$, it is a symmetric matrix. It is also bounded since it is continuous over a compact set. Thus a sufficient requirement is that ${J^{\prime\prime}}$ be positive definite on ${\hat \Theta}$. Positive definiteness of ${J^{\prime\prime}}$ can be viewed as ``positive curvature'' of $J$ at each point of ${\hat \Theta}$ which corresponds to strict concavity of $J$ on ${\hat \Theta}$.