Theorem. (Taylor) Every functional
![]() in
in
![]() has the representation
has the representation
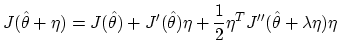
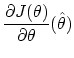 |
(5) | ||
 |
(6) |
Proof. See Goldstein [2] p. 119. The Taylor infinite series is treated in Williamson and Crowell [7]. The present form is typically more useful for computing bounds on the error incurred by neglecting higher order terms in the Taylor expansion.