Newton's Method

The gradient method is based on the first-order term in the Taylor expansion for $J({\hat \theta})$. By taking a second-order term as well and solving the quadratic minimization problem iteratively, Newton's method for functional minimization is obtained. Essentially, Newton's method requires the error surface to be close to quadratic, and its effectiveness is directly tied to the accuracy of this assumption. For most problems, the error surface can be well approximated by a quadratic form near the solution. For this reason, Newton's method tends to give very rapid (``quadratic'') convergence in the last stages of iteration.

Newton's method is derived as follows: The Taylor expansion of $J(\theta)$ about ${\hat \theta}$ gives

$$J({\hat \theta}^\ast ) = J({\hat \theta}) + J^\prime({\hat \theta... ...e{\lambda}{\hat \theta}\right) \left({\hat \theta}^\ast -{\hat \theta}\right),$$

for some $0\leq \lambda \leq 1$, where $\overline{\lambda}\mathrel{\stackrel{\mathrm{\Delta}}{=}}1-\lambda$. It is now necessary to assume that ${J^{\prime\prime}}\left(\lambda{\hat \theta}^\ast +\overline{\lambda}{\hat \theta}\right)\approx {J^{\prime\prime}}({\hat \theta})$. Differentiating with respect to ${\hat \theta}^\ast$, where $J({\hat \theta}^\ast )$ is presumed to be minimum, this becomes

$$0 = 0 + J^\prime({\hat \theta}) + {J^{\prime\prime}}({\hat \theta}) \left({\hat \theta}^\ast -{\hat \theta}\right).$$

Solving for ${\hat \theta}^\ast$ yields

$${\hat \theta}^\ast = {\hat \theta}- [{J^{\prime\prime}}({\hat \theta})]^{-1} J^\prime({\hat \theta}).$$ (7)

Applying Eq. (7) iteratively, we obtain the following.

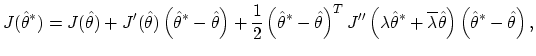
Definition. Newton's method is defined by

$${\hat \theta}_{n+1} = {\hat \theta}_n - [{J^{\prime\prime}}({\hat \theta}_n)]^{-1} J^\prime({\hat \theta}_n), \quad n=1,2,\ldots\,,$$ (8)

where ${\hat \theta}_0$ is given as an initial condition.

When ${J^{\prime\prime}}\left(\lambda{\hat \theta}^\ast +\overline{\lambda}{\hat \theta}\right)= {J^{\prime\prime}}({\hat \theta})$, the answer is obtained after the first iteration. In particular, when the error surface $J({\hat \theta})$ is a quadratic form in ${\hat \theta}$, Newton's method produces ${\hat \theta}^\ast$ in one iteration, i.e., ${\hat \theta}_1={\hat \theta}^\ast$ for every ${\hat \theta}_0$.

For Newton's method, there is the following general result on the existence of a critical point (i.e., a point at which the gradient vanishes) within a sphere of a Banach space.

Theorem. (Kantorovich) Let ${\hat \theta}_0$ be a point in ${\hat \Theta}$ for which $[{J^{\prime\prime}}({\hat \theta}_0)]^{-1}$ exists, and set

$$R_0 \mathrel{\stackrel{\mathrm{\Delta}}{=}}\left\Vert\,[{J^{\prime\prime}}({\hat \theta}_0)]^{-1}{J^\prime}({\hat \theta}_0)\,\right\Vert.$$

Let $S$ denote the sphere $\{{\hat \theta}\in{\hat \Theta}$ such that $\vert\vert\,{\hat \theta}-{\hat \theta}_0\,\vert\vert \leq 2R_0\}$. Set $C_0= \vert\vert\,{J^{\prime\prime}}({\hat \theta}_0)\,\vert\vert$. If there exists a number $M$ such that

$$\left\Vert\,{J^{\prime\prime}}({\hat \theta}_1)-{J^{\prime\prime}... ...ert \leq \frac{M\left\Vert\,{\hat \theta}_1-{\hat \theta}_2\,\right\Vert}{ 2},$$

for ${\hat \theta}_1,{\hat \theta}_2$ in $S$, and such that $C_0 R_0 M \mathrel{\stackrel{\mathrm{\Delta}}{=}}h_0\leq 1/2$, then ${J^\prime}({\hat \theta})=0$ for some ${\hat \theta}$ in $S$, and the Newton sequence Eq. (8) converges to it. Furthermore, the rate of convergence is quadratic, satisfying

$$\left\Vert\,{\hat \theta}^\ast -{\hat \theta}_n\,\right\Vert\leq 2^{-n+1}(2h_0)^{2^n-1}R_0.$$

Proof. See Goldstein [2], p. 143.