The impedance of a mass in the frequency domain is
In the
where the ``a'' subscript denotes ``analog''. For simplicity, let's choose the free constant
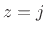
where the ``d'' subscript denotes ``digital. Multiplying through by the denominator and applying the shift theorem for
![\begin{eqnarray*}
(1+z^{-1})F_d(z) &=& M (1-z^{-1}) V_d(z) \\
\;\longleftrightarrow\;f_d(n) + f_d(n-1) &=& M[v_d(n) - v_d(n-1)] \\
\,\,\Rightarrow\,\,f_d(n) &=& M[v_d(n) - v_d(n-1)] - f_d(n-1).
\end{eqnarray*}](img1694.png)
This difference equation is diagrammed in Fig. 7.16. We recognize this recursive digital filter as the direct form I structure. The direct-form II structure is obtained by commuting the feedforward and feedback portions and noting that the two delay elements contain the same value and can therefore be shared [452]. The two other major filter-section forms are obtained by transposing the two direct forms by exchanging the input and output, and reversing all arrows. (This is a special case of Mason's Gain Formula which works for the single-input, single-output case.) When a filter structure is transposed, its summers become branching nodes and vice versa. Further discussion of the four basic filter section forms can be found in [336].
![\includegraphics[width=4in]{eps/lmassFilterDF1}](img1695.png) |