Direct-Form I

As mentioned in §5.5, the difference equation

$$y(n) = b_0 x(n) + b_1 x(n - 1) + \cdots + b_M x(n - M)$$

$$\qquad - a_1 y(n - 1) - \cdots - a_N y(n - N)$$

$$= \sum_{i=0}^M b_i x(n-i) - \sum_{j=1}^N a_j y(n-j)$$ (10.1)

specifies the Direct-Form I (DF-I) implementation of a digital filter [60]. The DF-I signal flow graph for the second-order case is shown in Fig.9.1.

Figure 9.1: Direct-Form-I implementation of a 2nd-order digital filter.

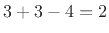The DF-I structure has the following properties:

1. It can be regarded as a two-zero filter section followed in series by a two-pole filter section.

2. In most fixed-point arithmetic schemes (such as two's complement, the most commonly used [84]^10.1) there is no possibility of internal filter overflow. That is, since there is fundamentally only one summation point in the filter, and since fixed-point overflow naturally ``wraps around'' from the largest positive to the largest negative number and vice versa, then as long as the final result $y(n)$ is ``in range'', overflow is avoided, even when there is overflow of intermediate results in the sum (see below for an example). This is an important, valuable, and unusual property of the DF-I filter structure.

3. There are twice as many delays as are necessary. As a result, the DF-I structure is not canonical with respect to delay. In general, it is always possible to implement an $N$ th-order filter using only $N$ delay elements.

4. As is the case with all direct-form filter structures (those which have coefficients given by the transfer-function coefficients), the filter poles and zeros can be very sensitive to round-off errors in the filter coefficients. This is usually not a problem for a simple second-order section, such as in Fig.9.1, but it can become a problem for higher order direct-form filters. This is the same numerical sensitivity that polynomial roots have with respect to polynomial-coefficient round-off. As is well known, the sensitivity tends to be larger when the roots are clustered closely together, as opposed to being well spread out in the complex plane [18, p. 246]. To minimize this sensitivity, it is common to factor filter transfer functions into series and/or parallel second-order sections, as discussed in §9.2 below.

It is a very useful property of the direct-form I implementation that it cannot overflow internally in two's complement fixed-point arithmetic: As long as the output signal is in range, the filter will be free of numerical overflow. Most IIR filter implementations do not have this property. While DF-I is immune to internal overflow, it should not be concluded that it is always the best choice of implementation. Other forms to consider include parallel and series second-order sections (§9.2 below), and normalized ladder forms [32,48,86].^10.2Also, we'll see that the transposed direct-form II (Fig.9.4 below) is a strong contender as well.