Like Rader's FFT, Bluestein's FFT algorithm (also known as the
chirp ![]() -transform algorithm), can be used to compute
prime-length DFTs in
-transform algorithm), can be used to compute
prime-length DFTs in
![]() operations
[25, pp. 213-215].A.6 However,
unlike Rader's FFT, Bluestein's algorithm is not restricted to prime
lengths, and it can compute other kinds of transforms, as discussed
further below.
operations
[25, pp. 213-215].A.6 However,
unlike Rader's FFT, Bluestein's algorithm is not restricted to prime
lengths, and it can compute other kinds of transforms, as discussed
further below.
Beginning with the DFT

where
![\begin{eqnarray*}
X(k)
&=&
\sum_{n=0}^{N-1}x(n)W^{-kn}W^{\frac{1}{2}(n^2+k^2)}W^{-\frac{1}{2}(n^2+k^2)}\\
&=& W^{-\frac{1}{2}k^2}
\sum_{n=0}^{N-1} \left[x(n)W^{-\frac{1}{2}n^2}\right]W^{\frac{1}{2}(k-n)^2} \\
&=& W^{-\frac{1}{2}k^2} (x_q \ast w_q)_k,
\end{eqnarray*}](img1644.png)
where `![]() ' denotes convolution (§7.2.4), and
the sequences
' denotes convolution (§7.2.4), and
the sequences ![]() and
and ![]() are defined by
are defined by
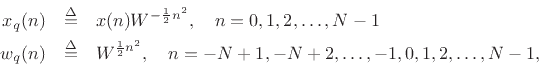
where the ranges of ![]() given are those actually required by the
convolution sum above. Beyond these required minimum ranges for
given are those actually required by the
convolution sum above. Beyond these required minimum ranges for ![]() ,
the sequences may be extended by zeros. As a result, we may implement
this convolution (which is cyclic for even
,
the sequences may be extended by zeros. As a result, we may implement
this convolution (which is cyclic for even ![]() and ``negacyclic'' for
odd
and ``negacyclic'' for
odd ![]() ) using zero-padding and a larger cyclic convolution, as
mentioned in §7.2.4. In particular, the larger cyclic
convolution size
) using zero-padding and a larger cyclic convolution, as
mentioned in §7.2.4. In particular, the larger cyclic
convolution size
![]() may be chosen a power of 2, which need
not be larger than
may be chosen a power of 2, which need
not be larger than ![]() . Within this larger cyclic convolution, the
negative-
. Within this larger cyclic convolution, the
negative-![]() indexes map to
indexes map to
![]() in the usual way.
in the usual way.
Note that the sequence ![]() above consists of the original data
sequence
above consists of the original data
sequence ![]() multiplied by a signal
multiplied by a signal
![]() which can be
interpreted as a sampled complex sinusoid with instantaneous
normalized radian frequency
which can be
interpreted as a sampled complex sinusoid with instantaneous
normalized radian frequency ![]() , i.e., an instantaneous
frequency that increases linearly with time. Such signals are called
chirp signals. For this reason, Bluestein's algorithm is also
called the chirp
, i.e., an instantaneous
frequency that increases linearly with time. Such signals are called
chirp signals. For this reason, Bluestein's algorithm is also
called the chirp ![]() -transform algorithm [62].
-transform algorithm [62].
In summary, Bluestein's FFT algorithm provides complexity ![]() for any positive integer DFT-length
for any positive integer DFT-length ![]() whatsoever, even when
whatsoever, even when ![]() is
prime.
is
prime.
Other adaptations of the Bluestein FFT algorithm can be used to
compute a contiguous subset of DFT frequency samples (any uniformly
spaced set of samples along the unit circle), with ![]() complexity. It can similarly compute samples of the
complexity. It can similarly compute samples of the ![]() transform
along a sampled spiral of the form
transform
along a sampled spiral of the form ![]() , where
, where ![]() is any complex
number, and
is any complex
number, and
![]() , again with complexity
, again with complexity ![]() [25].
[25].