Lossy Digital Waveguides

Let us now approach the simulation of propagation in lossy media which are represented by equation (26). We treat the one-dimensional scalar case here in order to focus on the kinds of filters that should be designed to embed losses in digital waveguide networks [44,25].

As usual, by inserting the exponential eigensolution into the wave equation, we get the one-variable version of (29)

$$\frac{s^2}{c^2} + s \Upsilon = V^2$$ (44)

where $V$ is the wave number, or spatial frequency, and it represents the wave length and attenuation in the direction of propagation.

Reconsidering the treatment of section III-A and reducing it to the scalar case, let us derive from (33) and (34) the expression for ${\mbox{\boldmath$\Theta$}}$

$$\Theta = \frac{1}{2} \Upsilon \omega_s \vert V_I \vert ^{-2} \; ,$$ (45)

which gives the unique solution for (33)

$$\Theta = - \frac{\omega_s}{\Upsilon c^2} + \sqrt{\frac{{\omega_s}^2}{\Upsilon^2 c^4} + 1} \; .$$ (46)

This shows us that the exponential attenuation in (32) is frequency dependent, and we can even plot the real and imaginary parts of the wave number $V$ as functions of frequency, as reported in Fig. 2.

Figure 2: Imaginary and real part of the wave number as functions of frequency ( $\Upsilon = 0.001$)

If the frequency range of interest is above a certain threshold, i.e., ${\Upsilon c^2}/{\omega_s}$ is small, we can obtain the following relations from (47), by means of a Taylor expansion truncated at the first term:

$$\left\{ \begin{array}{l} \vert{v}_I\vert \simeq \frac{\omega... ...R\vert \simeq \frac{1}{ 2} \Upsilon c \; . \end{array}\right.$$ (47)

Namely, for sufficiently high frequencies, the attenuation can be considered to be constant and the dispersion relation can be considered to be the same as in a non-dissipative medium, as it can be seen from Fig. 2.

Still under the assumption of small losses, and truncating the Taylor expansion of $\Theta$ to the first term, we find that the wave admittance (35) reduces to the two ``directional admittances'':

$$\begin{array}{l} \Gamma^+ \stackrel{\triangle}{=}\Gamma(s) =... ...-}{p^-} = G_0 \left( -1 +\frac{1}{s L} \right) \; , \end{array}$$ (48)

where $G_0 = \frac{1}{\mu c}$ is the admittance of the medium without losses, and $L=-\frac{2}{\Upsilon c^2}$ is a negative shunt reactance that accounts for losses.

The actual wave admittance of a one-dimensional medium, such as a tube, is $\Gamma(s)$ while $\Gamma^*(-s^*)$ is its paraconjugate in the analog domain. Moving to the discrete-time domain by means of a bilinear transformation, it is easy to verify that we get a couple of ``directional admittances'' that are related through (21).

In the case of the dissipative tube, as we expect, wave propagation is not lossless, since . However, the medium is passive in the sense of section II-E, since the sum is positive semidefinite along the imaginary axis.

The relations here reported hold for any one-dimensional resonator with frictional losses. Therefore, they hold for a certain class of dissipative strings and tubes. Remarkably similar wave admittances are also found for spherical waves propagating in conical tubes (see Appendix A).

The simulation of a length-$L_R$ section of lossy resonator can proceed according to two stages of approximation. If the losses are small (i.e., $\Upsilon \approx 0$) the approximation (48) can be considered valid in all the frequency range of interest. In such case, we can lump all the losses of the section in a single coefficient $g_L = e^{\frac{1}{2} \Upsilon c L_R}$. The resonator can be simulated by the structure of Fig. 3, where we have assumed that the length $L_R$ is equal to an integer number $m_L$ of spatial samples.

Figure: Length-$L_R$ one-variable waveguide section with small losses

At a further level of approximation, if the values of $\Upsilon$ are even smaller we can consider the reactive component of the admittance to be zero, thus assuming $\Gamma^+ = \Gamma^- = G_0$.

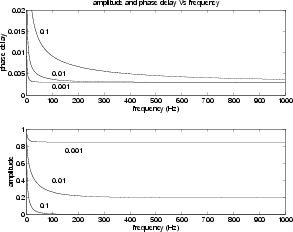
On the other hand, if losses are significant, we have to represent wave propagation in the two directions with a filter whose frequency response can be deduced from Fig. 2. In practice, we have to insert a filter $G_L$ having magnitude and phase delay that are represented in Fig. 4 for different values of $\Upsilon$. From such filter we can subtract a contribution of linear phase, which can be implemented by means of a pure delay.

Figure 4: Magnitude and phase delay introduced by frictional losses in a waveguide section of length $L_R=1$, for different values of $\Upsilon$