With a further generalization, we can consider losses that are dependent on frequency, so that the friction coefficient ![]() is replaced by
is replaced by
![]() . In such case, all the formulas up to (49) will be recomputed with this new
. In such case, all the formulas up to (49) will be recomputed with this new
![]() .
.
Quite often, losses are deduced from experimental data which give the value ![]() . In these cases, it is useful to calculate the value of
. In these cases, it is useful to calculate the value of
![]() so that the wave admittance can be computed.
From (33) we find
so that the wave admittance can be computed.
From (33) we find
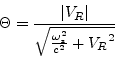 |
(51) |
For instance, in a radius-![]() cylindrical tube, the visco-thermal losses can be approximated by the formula [45]
cylindrical tube, the visco-thermal losses can be approximated by the formula [45]
| (53) |
In vibrating strings, the viscous friction with air determines a damping that can be represented by the formula [45]
| (54) |
<1334>>