Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Multivariable Formulation
The 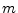 -variable lossy wave equation is
-variable lossy wave equation is
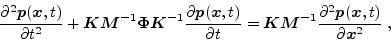 |
(25) |
where
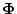 is a
is a 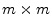 matrix that represents a viscous resistance.
If we plug the eigensolution (10) into (26), we get, in the Laplace domain
matrix that represents a viscous resistance.
If we plug the eigensolution (10) into (26), we get, in the Laplace domain
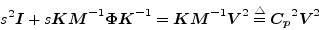 |
(26) |
or, by letting
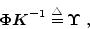 |
(27) |
we get
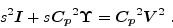 |
(28) |
By restricting the Laplace analysis to the imaginary (frequency) axis
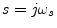 , decomposing the (diagonal) spatial frequency matrix into its real and imaginary parts
, decomposing the (diagonal) spatial frequency matrix into its real and imaginary parts
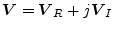 , and equating the real and imaginary parts of equation (29), we get the equations
, and equating the real and imaginary parts of equation (29), we get the equations
The term
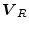 can be interpreted as attenuation per unit length, while
can be interpreted as attenuation per unit length, while
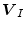 keeps the role of spatial frequency, so that the traveling wave solution is
keeps the role of spatial frequency, so that the traveling wave solution is
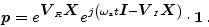 |
(31) |
Defining
 as the ratio
as the ratio![[*]](../icons/footnote.png) between the real and imaginary parts of
between the real and imaginary parts of
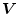 (
(
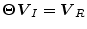 ), the equations (30) and (31) become
), the equations (30) and (31) become
Following steps analogous to those of eq. (18),
the 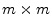 admittance matrix turns out to be
admittance matrix turns out to be
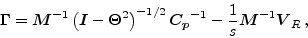 |
(34) |
which, for
 , collapses to the reciprocal of (19).
For the discrete-time case, we may map
, collapses to the reciprocal of (19).
For the discrete-time case, we may map
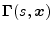 from the
from the  plane to
the
plane to
the 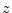 plane via the bilinear transformation [43], or we may
sample the inverse Laplace transform of
plane via the bilinear transformation [43], or we may
sample the inverse Laplace transform of
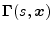 and take its
and take its 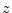 transform
to obtain
transform
to obtain
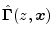 .
.
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download gdwn.pdf
![]() admittance matrix turns out to be
admittance matrix turns out to be