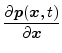 |
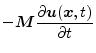 |
(5) | |
 |
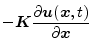 |
(6) |
Perhaps the most straightforward multivariable generalization of
(2) and (3) is
| (8) |
Similarly, differentiating (5) with respect to ![]() and
(6) with respect to
and
(6) with respect to
![]() , and eliminating
, and eliminating
![]() yields
yields
For digital waveguide modeling, we desire solutions of the
multivariable wave equation involving only sums of traveling waves.
Consider the eigenfunction
Similarly, applying (10) to (9) yields
Having established that (13) is a solution of
(7) when condition (11) holds on the matrices
![]() and
and
![]() , we can express the general traveling-wave
solution to (7) in both pressure and velocity as
, we can express the general traveling-wave
solution to (7) in both pressure and velocity as
When the mass and tension matrices
![]() and
and
![]() are
diagonal, our analysis corresponds to considering
are
diagonal, our analysis corresponds to considering ![]() separate
waveguides as a whole. For example, the two transversal planes of
vibration in a string can be described by (7) with
separate
waveguides as a whole. For example, the two transversal planes of
vibration in a string can be described by (7) with
![]() . In a musical instrument such as the piano [29],
the coupling among the strings and between different vibration
modalities within a single string, occurs primarily at the
bridge [30]. Indeed, the bridge acts like a junction of
several multivariable waveguides (see section IV).
. In a musical instrument such as the piano [29],
the coupling among the strings and between different vibration
modalities within a single string, occurs primarily at the
bridge [30]. Indeed, the bridge acts like a junction of
several multivariable waveguides (see section IV).
When the matrices
![]() and
and
![]() are
non-diagonal, the physical interpretation can be of the form
are
non-diagonal, the physical interpretation can be of the form
Besides
the existence of physical systems that support multivariable traveling
wave solutions, there are other practical reasons for considering a
multivariable formulation of wave propagation. For instance, modal
analysis considers the vector
![]() (whose dimension is infinite in general)
of coefficients of the normal mode expansion of the system response. For spaces in perfectly reflecting
enclosures,
(whose dimension is infinite in general)
of coefficients of the normal mode expansion of the system response. For spaces in perfectly reflecting
enclosures,
![]() can be compacted so that each element accounts for all the modes sharing the same spatial dimension [32].
can be compacted so that each element accounts for all the modes sharing the same spatial dimension [32].
![]() admits a wave decomposition as
in (16), and
admits a wave decomposition as
in (16), and
![]() is diagonal. Having walls with
finite impedance, there is a damping term proportional to
is diagonal. Having walls with
finite impedance, there is a damping term proportional to
![]() that functions as a coupling term
among the ideal modes [33]. Coupling among the modes can also be exerted by diffusive properties of the enclosure [32,9].
that functions as a coupling term
among the ideal modes [33]. Coupling among the modes can also be exerted by diffusive properties of the enclosure [32,9].
Note that the multivariable wave equation (7)
considered here does not include wave equations governing propagation
in multidimensional media (such as membranes, spaces, and solids). In
higher dimensions, the solution in the ideal linear lossless case is a
superposition of waves traveling in all directions in the
![]() -dimensional space [27]. However, it turns out that a good
simulation of wave propagation in a multidimensional medium may in
fact be obtained by forming a mesh of unidirectional
waveguides as considered here, each described by (7);
such a mesh of 1D waveguides can be shown to solve numerically a
discretized wave equation for multidimensional media
[34,35,13,14].
-dimensional space [27]. However, it turns out that a good
simulation of wave propagation in a multidimensional medium may in
fact be obtained by forming a mesh of unidirectional
waveguides as considered here, each described by (7);
such a mesh of 1D waveguides can be shown to solve numerically a
discretized wave equation for multidimensional media
[34,35,13,14].