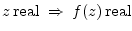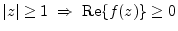- ... III
![[*]](../icons/footnote.png)
- D. Rocchesso is with the Dipartimento di Informatica,
Università degli Studi di Verona, strada Le Grazie, 37134 Verona - ITALY,
Phone: ++39.045.8027979, FAX: ++39.045.8027982, E-mail:
rocchesso@sci.univr.it. J. O. Smith is with
the Center for Computer Research in Music and Acoustics (CCRMA), Music
Department, Stanford University, Stanford, CA 94305, E-mail:
jos@ccrma.stanford.edu.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
``tension
![[*]](../icons/footnote.png)
- ``Tension'' is defined here for gases as the
reciprocal of the adiabatic compressibility of the gas
[28, p. 230]. This definition helps to unify the
scattering formalism for acoustic tubes with that of mechanical
systems such as vibrating strings.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... tube
![[*]](../icons/footnote.png)
- There appear to be no tube shapes
supporting exact traveling waves other than cylindrical and conical
(or conical wedge, which is a hybrid) [36]. However, the
``Salmon horn family'' (see, e.g., [27,37])
characterizes a larger class of approximate one-parameter
traveling waves. In the cone, the wave equation is solved for
pressure
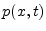 using a change of variables
using a change of variables
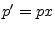 , where
, where
 is the distance from the apex of the cone, causing the wave
equation for the cone pressure to reduce to the cylindrical case
[38]. Note that while pressure waves behave simply as non-dispersive
traveling waves in cones, the corresponding velocity waves are dispersive [38].
is the distance from the apex of the cone, causing the wave
equation for the cone pressure to reduce to the cylindrical case
[38]. Note that while pressure waves behave simply as non-dispersive
traveling waves in cones, the corresponding velocity waves are dispersive [38].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... power
![[*]](../icons/footnote.png)
- Note
that
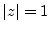 corresponds to the average physical power at frequency
corresponds to the average physical power at frequency 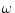 ,
where
,
where
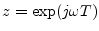 , and the wave variable magnitudes on the unit circle
may be interpreted as RMS levels. For
, and the wave variable magnitudes on the unit circle
may be interpreted as RMS levels. For 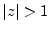 , we may interpret
the power
, we may interpret
the power
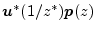 as the steady state power obtained when exponential
damping is introduced into the waveguide giving decay time-constant
as the steady state power obtained when exponential
damping is introduced into the waveguide giving decay time-constant 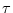 ,
where
,
where
 (for the continuous-time case, see [40, p. 48]).
(for the continuous-time case, see [40, p. 48]).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... real
![[*]](../icons/footnote.png)
- A complex-valued function
of a complex variable
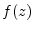 is said to be positive real if
is said to be positive real if
- 1)
-
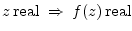
- 2)
-
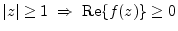
Positive real functions characterize passive impedances in classical network theory.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ratio
![[*]](../icons/footnote.png)
- Indeed, in the general case
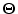 is a diagonal matrix.
is a diagonal matrix.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... velocity
![[*]](../icons/footnote.png)
- The symbols for the variables
velocity and force have been chosen to maintain consistency with the
analogous acoustical quantities.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.