Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
The net complex power involved in the propagation can be
defined as [40]
where all quantities above are functions of 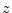 as in (21).
The quantity
as in (21).
The quantity
 is called right-going active power (or right-going average dissipated power
is called right-going active power (or right-going average dissipated power![[*]](../icons/footnote.png) ),
while
),
while
 is called the left-going active
power. The term
is called the left-going active
power. The term 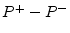 , the right-going minus the left-going power
components, we call the net active power, while the term
, the right-going minus the left-going power
components, we call the net active power, while the term
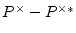 is net reactive power.
These names all stem from the case in which the matrix
is net reactive power.
These names all stem from the case in which the matrix
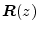 is positive definite for
is positive definite for 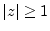 . In this case, both the
components of the active power are real and positive, the active power itself is real,
while the reactive power is purely imaginary.
. In this case, both the
components of the active power are real and positive, the active power itself is real,
while the reactive power is purely imaginary.
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download gdwn.pdf