An Efficient Class of Loss Filters

A first-order IIR filter that, when cascaded with a delay line, simulates wave propagation in a lossy resonator of length $L_R$, can take the form

$$G_L(z) = \left( \alpha \frac{1-r}{1-r z^{-1}} + (1 - \alpha) \right) z^{-L_R F_s / c}$$

$$\stackrel{\triangle}{=}H_L(z) z^{-L_R F_s / c} \: .$$ (49)

At the Nyquist frequency, and for $r\simeq 1$, such filter gains $G_L(e^{j \pi}) \simeq 1 - \alpha$ and we have to use $\alpha = 1 - e^{-\frac{1}{2}\Upsilon c L_R}$ to have the correct attenuation at high frequency. Fig. 5 shows the magnitude and phase delay (in seconds) obtained with the first-order filter $G_L$ for three values of its parameter $r$.

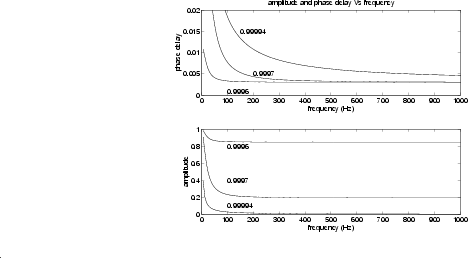
By comparison of the curves of Fig. 4 with the responses of Fig. 5, we see how the latter can be used to represent the losses in a section of one-dimensional waveguide section. Therefore, the simulation scheme turns out to be that of Fig. 6. Of course, better approximations of the curves of Fig. 4 can be obtained by increasing the filter order or, at least, by controlling the zero position of a first-order filter. However, the form (50) is particularly attractive because its low-frequency behavior is controlled by the single parameter $r$.

Figure 5: Magnitude and phase delay of a first-order IIR filter, for different values of the coefficient $r$, $\alpha$ is set to $1 - e^{-\frac{1}{2}\Upsilon c L_R }$ with the same values of $\Upsilon$ used for the curves in fig. 4

Figure: Length-$L_R$ one-variable waveguide section with small losses

As far as the wave impedance is concerned, in the discrete-time domain, it can be represented by a digital filter obtained from (49) by bilinear transformation, which leads to

$$R^+ = \frac{2 L F_s}{G_0} \frac{1 - z^{-1}}{2 L F_s + 1 - (2 L F_s - 1)z^{-1}} \; ,$$ (50)

that is a first-order high-pass filter. The discretization by impulse invariance can not be applied in this case because the impedance has a high-frequency response that would alias heavily.