In this section, we will find the frequency response of the simplest lowpass filter
using simulated sine-wave analysis carried out by a matlab program. This numerical approach complements the analytical approach followed in §1.3. Figure 2.3 gives a listing of the main script which invokes the sine-wave analysis function swanal listed in Fig.
% swanalmain.m - matlab program for simulated sinewave % analysis on the simplest lowpass filter: % % y(n) = x(n)+x(n-1)} B = [1,1]; % filter feedforward coefficients A = 1; % filter feedback coefficients (none) N = 10; % number of sinusoidal test frequencies fs = 1; % sampling rate in Hz (arbitrary) T = 1/fs; % sampling interval in seconds fmax = fs/2; % highest frequency to look at df = fmax/(N-1);% spacing between frequencies f = 0:df:fmax; % sampled frequency axis tmax = 1/df; % 1 cycle at lowest non-dc freq t = 0:T:tmax; % sampled time axis % [gains,phases] = swanal(t,f,fs,B,A); % sinewave analysis swanal; % configured for ease of variable inspection plotfile = '../eps/swanalmain.eps'; swanalmainplot; % final plots and comparison to theory |
In the swanal function (Fig.![]() ), test
sinusoids are generated by the line
), test
sinusoids are generated by the line
s = ampin * cos(2*pi*f(k)*t + phasein);
where amplitude, frequency (Hz), and phase (radians) of the sinusoid are given be
ampin, f(k), and phasein, respectively. As discussed
in §1.3, assuming linearity and time-invariance (LTI) allows
us to set
ampin = 1; % input signal amplitude
phasein = 0; % input signal phase
without loss of generality. (Note that we must also assume the filter
is LTI for sine-wave analysis to be a general method for
characterizing the filter's response.) The test sinusoid is passed
through the digital filter by the line
y = filter(B,A,s); % run s through the filter
producing the output signal in vector y. For this example
(the simplest lowpass filter), the filter coefficients are simply
B = [1,1]; % filter feedforward coefficients
A = 1; % filter feedback coefficients (none)
The coefficient A(1) is technically a coefficient on the
output signal itself, and it should always be normalized to 1.
(B and A can be multiplied by the same nonzero constant to
carry out this normalization when necessary.)
Figure 2.4 shows one of the intermediate plots produced by the
sine-wave analysis routine in Fig.![]() . This figure corresponds
to Fig.1.6 in §1.3 (see page
. This figure corresponds
to Fig.1.6 in §1.3 (see page ![]() ). In
Fig.2.4a, we see samples of the input test sinusoid overlaid
with the continuous sinusoid represented by those
samples. Figure 2.4b shows only the samples of the filter output
signal: While we know the output signal becomes a sampled sinusoid
after the one-sample transient response, we do not know its amplitude
or phase until we measure it; the underlying continuous signal
represented by the samples is therefore not plotted. (If we really
wanted to see this, we could use software for bandlimited
interpolation [91], such as Matlab's
interp function.) A plot such as Fig.2.4 is produced
for each test frequency, and the relative amplitude and phase are
measured between the input and output to form one sample of the
measured frequency response, as discussed in
§1.3.
). In
Fig.2.4a, we see samples of the input test sinusoid overlaid
with the continuous sinusoid represented by those
samples. Figure 2.4b shows only the samples of the filter output
signal: While we know the output signal becomes a sampled sinusoid
after the one-sample transient response, we do not know its amplitude
or phase until we measure it; the underlying continuous signal
represented by the samples is therefore not plotted. (If we really
wanted to see this, we could use software for bandlimited
interpolation [91], such as Matlab's
interp function.) A plot such as Fig.2.4 is produced
for each test frequency, and the relative amplitude and phase are
measured between the input and output to form one sample of the
measured frequency response, as discussed in
§1.3.
![\includegraphics[width=\twidth ]{eps/swanalsix}](img259.png) |
Next, the one-sample start-up transient is removed from the filter
output signal y to form the ``cropped'' signal yss
(``![]() steady state''). The final task is to measure the amplitude
and phase of the yss. Output amplitude estimation is done in
swanal by the line
steady state''). The final task is to measure the amplitude
and phase of the yss. Output amplitude estimation is done in
swanal by the line
[ampout,peakloc] = max(abs(yss));
Note that the peak amplitude found in this way is approximate,
since the true peak of the output sinusoid generally occurs
between samples. We will find the output amplitude much
more accurately in the next two sections. We store the index of the
amplitude peak in peakloc so it can be used to estimate phase
in the next step. Given the output amplitude ampout, the
amplitude response of the filter at frequency f(k) is
given by
gains(k) = ampout/ampin;
The last step of swanal in Fig.
phaseDiff = acos(min(1,max(-1,yss(end)/ampOut))) ...
- acos(min(1,max(-1,sss(end)/ampIn)));
phaseDiff = mod2pi(phaseDiff); % reduce to [-pi,pi)
The mod2pi utility reduces
its scalar argument to the range
function [y] = mod2pi(x) % MOD2PI - Reduce x to the range [-pi,pi) y=x; twopi = 2*pi; while y >= pi, y = y - twopi; end while y < -pi, y = y + twopi; end |
In summary, the sine-wave analysis measures experimentally the gain and phase-shift of the digital filter at selected frequencies, thus measuring the frequency response of the filter at those frequencies. It is interesting to compare these experimental results with the closed-form expressions for the frequency response derived in §1.3.2. From Equations (1.6-1.7) we have
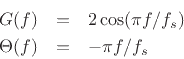
where ![]() denotes the amplitude response (filter gain versus
frequency),
denotes the amplitude response (filter gain versus
frequency), ![]() denotes the phase response (filter
phase-shift versus frequency),
denotes the phase response (filter
phase-shift versus frequency), ![]() is frequency in Hz, and
is frequency in Hz, and ![]() denotes the sampling rate. Both the amplitude response and phase
response are real-valued functions of (real) frequency, while
the frequency response is the complex function of
frequency given by
denotes the sampling rate. Both the amplitude response and phase
response are real-valued functions of (real) frequency, while
the frequency response is the complex function of
frequency given by
![]() .
.
Figure 2.6 shows overlays of the measured and theoretical results. While there is good general agreement, there are noticeable errors in the measured amplitude- and phase-response curves. While we know the input sinusoidal amplitude exactly because we generated it synthetically, the filter output amplitude was crudely approximated as the largest sample magnitude observed, without interpolation to better estimate the true peak amplitude. Phase-response errors are in turn caused by output-amplitude errors.
It is important to understand the source(s) of deviation between the measured and theoretical values. Our simulated sine-wave analysis deviates from an ideal sine-wave analysis in the following ways (listed in ascending order of importance):
The need for interpolation is lessened greatly if the sampling rate is
chosen to be unrelated to the test frequencies (ideally so that the
number of samples in each sinusoidal period is an irrational number).
Figure 2.7 shows the measured and theoretical results obtained
by changing the highest test frequency fmax from ![]() to
to
![]() , and the number of samples in each test sinusoid
tmax from
, and the number of samples in each test sinusoid
tmax from ![]() to
to ![]() . For these parameters, at least one
sample falls very close to a true peak of the output sinusoid at each
test frequency.
. For these parameters, at least one
sample falls very close to a true peak of the output sinusoid at each
test frequency.
It should also be pointed out that one never estimates signal phase in practice by inverting the closed-form functional form assumed for the signal. Instead, we should estimate the delay of each output sinusoid relative to the corresponding input sinusoid. This leads to the general topic of time delay estimation [12]. Under the assumption that the round-off error can be modeled as ``white noise'' (typically this is an accurate assumption), the optimal time-delay estimator is obtained by finding the (interpolated) peak of the cross-correlation between the input and output signals. For further details on cross-correlation, a topic in statistical signal processing, see, e.g., [77,87].
Using the theory presented in later chapters, we will be able to compute very precisely the frequency response of any LTI digital filter without having to resort to bandlimited interpolation (for measuring amplitude response) or time-delay estimation (for measuring phase).