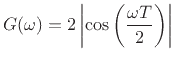Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
We can isolate the filter amplitude response  by squaring
and adding the above two equations:
by squaring
and adding the above two equations:
This can then be simplified as follows:
So we have made it to the amplitude response of the simple lowpass
filter
 :
:
Since
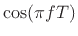 is nonnegative for
is nonnegative for
 , it
is unnecessary to take the absolute value as long as
, it
is unnecessary to take the absolute value as long as 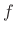 is understood
to lie in this range:
is understood
to lie in this range:
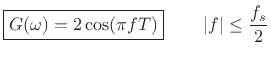 |
(2.6) |
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() by squaring
and adding the above two equations:
by squaring
and adding the above two equations:
![\begin{eqnarray*}
a^2(\omega) + b^2(\omega) &=& G^2(\omega)\cos^2[\Theta(\omega)] + G^2(\omega) \sin^2[\Theta(\omega)]\\
&=& G^2(\omega)\left\{\cos^2[\Theta(\omega)] + \sin^2[\Theta(\omega)]\right\}\\
&=& G^2(\omega).
\end{eqnarray*}](img161.png)
![\begin{eqnarray*}
G^2(\omega) &=& a^2(\omega) + b^2(\omega)\\
&=& [1 + \cos(\omega T)]^2 + \sin^2(\omega T) \\
&=& 1 + 2 \cos(\omega T) + \cos^2(\omega T) + \sin^2(\omega T)\\
&=& 2 + 2 \cos(\omega T) \\
&=&4 \cos^2\left(\frac{\omega T}{2}\right).
\end{eqnarray*}](img162.png)
![]() :
: