The quality factor (Q) of a real two-pole resonator may be
defined in terms of its complex one-pole components, where the
one-pole components have poles at
![]() and
and
![]() ; as discussed above, each of these
complex resonators has quality factor
; as discussed above, each of these
complex resonators has quality factor
![]() .
However, this is only accurate for their sum when the poles can be
treated as fully separated in frequency. In other words, we must
assume that the center-frequency and bandwidth of the complex
resonators are not significantly affected by summing their frequency
responses. In the high-Q case,
.
However, this is only accurate for their sum when the poles can be
treated as fully separated in frequency. In other words, we must
assume that the center-frequency and bandwidth of the complex
resonators are not significantly affected by summing their frequency
responses. In the high-Q case,
![]() , this
assumption is accurate. For greater accuracy, we should calculate
where the peak-gain frequency has moved, and what the modified
bandwidths may be.
, this
assumption is accurate. For greater accuracy, we should calculate
where the peak-gain frequency has moved, and what the modified
bandwidths may be.
Let's look at what happens when we add a one-pole complex resonator to its complex-conjugate counterpart to form a real second-order resonator:
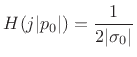
We see that a zero at
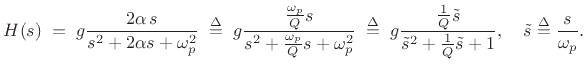
Since we always have
![]() for stability, it is convenient to
define the positive number
for stability, it is convenient to
define the positive number
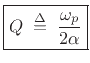
which is called the damping constant (or damping factor) for real, second-order resonators [20, p. 179]. The damping constant is simply minus the real part of the poles. (We are assuming the poles form a complex-conjugate pair--excluding the case of two different real poles.) A related term from mechanics is the damping ratio
We also have
That is,
The transfer function of the real second-order resonator with one zero
at dc and the other at infinity, with peak gain normalized to ![]() , can
be written in terms of our new notation as
, can
be written in terms of our new notation as
In view of the above, it is now reasonable to define the quality factor (Q) of the real second-order resonator Eq.(E.7) by [20, p. 184]
The peak-gain frequency ![]() (pole modulus) coincides with
the physical oscillation frequency
(pole modulus) coincides with
the physical oscillation frequency ![]() of the resonator impulse
response (pole imaginary part) when the damping constant
of the resonator impulse
response (pole imaginary part) when the damping constant ![]() is
zero. The physical oscillation frequency
is
zero. The physical oscillation frequency ![]() of the impulse
response remains (twice) the zero-crossing rate of the sinusoidal oscillation
underneath the exponential decay of the impulse response. See
also §B.6 for a discussion of discrete-time resonators.
of the impulse
response remains (twice) the zero-crossing rate of the sinusoidal oscillation
underneath the exponential decay of the impulse response. See
also §B.6 for a discussion of discrete-time resonators.