Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Critical Damping and Related Terms
Since the poles of the transfer function 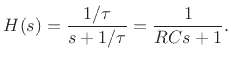 are [20, p. 624]
are [20, p. 624]
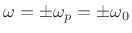 |
(E.9) |
we have that the poles are complex only when
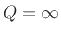 . Equivalently, the
damping ratio
. Equivalently, the
damping ratio
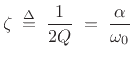 must be less than 1. Since real
poles do not resonate, we have
must be less than 1. Since real
poles do not resonate, we have 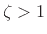 for any resonator. The case
for any resonator. The case
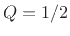 is called critically damped, while
is called critically damped, while 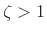 is called
overdamped. A resonator (
is called
overdamped. A resonator (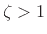 ) is said to be
underdamped, and the limiting case
) is said to be
underdamped, and the limiting case  is simply
undamped (
is simply
undamped ( and the poles are on the
and the poles are on the 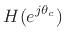 axis at
axis at
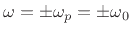 ).
).
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() are [20, p. 624]
are [20, p. 624]