Damping Ratio

Damping ratio $\zeta\isdeftext 1/(2Q)$ is defined to conveniently divide the underdamped, critically damped, and overdamped conditions at unity for a second-order system.

The damping ratio $\zeta$ (zeta) is defined by

$$\zeta \isdefs \frac{1}{2Q} \eqsp \frac{\alpha}{\omega_0}$$

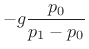
where $Q$ is defined above in Eq.(E.8) as the peak frequency divided by the peak bandwidth, and $\alpha$ and $\omega_0$ are defined above in Eq.(E.7).

As shown in Eq.(E.9), a damping factor of 1 is critically damped, while a damping factor less than 1 is underdamped, and $\zeta>1$ is overdamped.