Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Figure D.1 depicts a free mass driven by an external force along
an ideal frictionless surface in one dimension. Figure D.2
shows the electrical equivalent circuit for this scenario in
which the external force is represented by a voltage source emitting
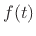 volts, and the mass is modeled by an inductor
having the value
volts, and the mass is modeled by an inductor
having the value 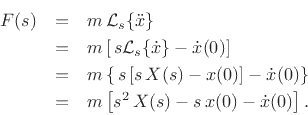 Henrys.
Henrys.
Figure D.1:
Physical diagram of an external force driving a mass
along a frictionless surface.
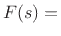 |
Figure D.2:
Electrical equivalent circuit of the
force-driven mass in Fig.D.1.
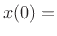 |
From Newton's second law of motion ``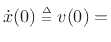 '', we have
'', we have
Taking the unilateral Laplace transform and applying the
differentiation theorem twice yields
Thus, given
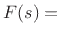 Laplace transform of the driving force
Laplace transform of the driving force 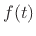 ,
,
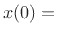 initial mass position, and
initial mass position, and
-
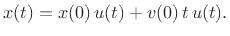 initial mass velocity,
initial mass velocity,
we can solve algebraically for  , the Laplace transform of the
mass position for all
, the Laplace transform of the
mass position for all  . This Laplace transform can then be
inverted to obtain the mass position
. This Laplace transform can then be
inverted to obtain the mass position 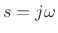 for all
for all  . This is
the general outline of how Laplace-transform analysis goes for
all linear, time-invariant (LTI) systems. For nonlinear and/or
time-varying systems, Laplace-transform analysis cannot, strictly
speaking, be used at all.
. This is
the general outline of how Laplace-transform analysis goes for
all linear, time-invariant (LTI) systems. For nonlinear and/or
time-varying systems, Laplace-transform analysis cannot, strictly
speaking, be used at all.
If the applied external force 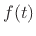 is zero, then, by linearity of
the Laplace transform, so is
is zero, then, by linearity of
the Laplace transform, so is 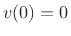 , and we readily obtain
, and we readily obtain
Since  is the unilateral Laplace transform of the Heaviside unit-step function
is the unilateral Laplace transform of the Heaviside unit-step function
and since 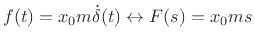 is the transform of
is the transform of 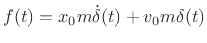 ,
we find that the position of the mass
,
we find that the position of the mass 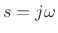 is given for all time by
is given for all time by
Thus, for example, a nonzero initial position 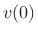 and zero
initial velocity
and zero
initial velocity 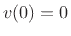 results in
results in 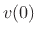 for all
for all  ; that
is, the mass ``just sits there''.D.3 Similarly, any initial velocity
; that
is, the mass ``just sits there''.D.3 Similarly, any initial velocity 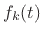 is integrated with
respect to time, meaning that the mass moves forever at the initial
velocity.
is integrated with
respect to time, meaning that the mass moves forever at the initial
velocity.
To summarize, this simple example illustrated use the Laplace
transform to solve for the motion of a simple physical system (an
ideal mass) in response to initial conditions (no external driving
forces). The system was described by a differential equation which
was converted to an algebraic equation by the Laplace transform.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() volts, and the mass is modeled by an inductor
having the value
volts, and the mass is modeled by an inductor
having the value ![]() Henrys.
Henrys.
![]() '', we have
'', we have
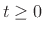
![\begin{eqnarray*}
F(s) &=& m\,{\cal L}_s\{{\ddot x}\}\\
&=& m\left[\,s {\cal L}_s\{{\dot x}\} - {\dot x}(0)\right]\\
&=& m\left\{\,s \left[s\,X(s) - x(0)\right] - {\dot x}(0)\right\}\\
&=& m\left[s^2\,X(s) - s\,x(0) - {\dot x}(0)\right].
\end{eqnarray*}](img1755.png)
![]() is zero, then, by linearity of
the Laplace transform, so is
is zero, then, by linearity of
the Laplace transform, so is ![]() , and we readily obtain
, and we readily obtain
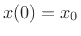
![$\displaystyle u(t)\isdef \left\{\begin{array}{ll}
0, & t<0 \\ [5pt]
1, & t\ge 0 \\
\end{array} \right.,
$](img1762.png)