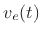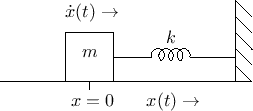Mass-Spring Oscillator Analysis

Consider now the mass-spring oscillator depicted physically in Fig.D.3, and in equivalent-circuit form in Fig.D.4.

Figure D.3: An ideal mass $m$ sliding on a frictionless surface, attached via an ideal spring $k$ to a rigid wall. The spring is at rest when the mass is centered at $x=0$ .

Figure D.4: Equivalent circuit for the mass-spring oscillator.

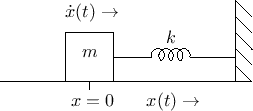By Newton's second law of motion, the force $f_m(t)$ applied to a mass equals its mass times its acceleration:

$$f_m(t)=m{\ddot x}(t).$$

By Hooke's law for ideal springs, the compression force $f_k(t)$ applied to a spring is equal to the spring constant $k$ times the displacement $x(t)$ :

$$f_k(t)=kx(t)$$

By Newton's third law of motion (``every action produces an equal and opposite reaction''), we have $f_k = -f_m$ . That is, the compression force $f_k$ applied by the mass to the spring is equal and opposite to the accelerating force $f_m$ exerted in the negative-$x$ direction by the spring on the mass. In other words, the forces at the mass-spring contact-point sum to zero:

$$\begin{eqnarray*} f_m(t) + f_k(t) &=& 0\\ \Rightarrow\; m {\ddot x}(t) + k x(t) &=& 0 \end{eqnarray*}$$

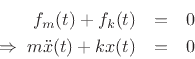
We have thus derived a second-order differential equation governing the motion of the mass and spring. (Note that $x(t)$ in Fig.D.3 is both the position of the mass and compression of the spring at time $t$ .)

Taking the Laplace transform of both sides of this differential equation gives

$$\begin{eqnarray*} 0 &=& {\cal L}_s\{m{\ddot x}+ k x\} \\ &=& m{\cal L}_s\{{\ddot x}\} + k {\cal L}_s\{x\} \quad \hbox{(by linearity)} \\ &=& m\left[s{\cal L}_s\{{\dot x}\} - {\dot x}(0)\right] + k X(s) \quad\hbox{(by the differentiation theorem)} \\ &=& m\left\{s\left[sX(s) - x(0)\right] - {\dot x}(0)\right\} + k X(s) \quad \hbox{(diff.~theorem again)} \\ &=& ms^2 X(s) - msx(0) - m{\dot x}(0) + k X(s). \end{eqnarray*}$$

To simplify notation, denote the initial position and velocity by $x(0)=x_0$ and ${\dot x}(0)={\dot x}_0=v_0$ , respectively. Solving for $X(s)$ gives

$$\begin{eqnarray*} X(s) &=& \frac{sx_0 + v_0}{s^2 + \frac{k}{m}} \;\isdef \; \frac{r}{s+j{\omega_0}} + \frac{\overline{r}}{s-j{\omega_0}},\quad {\omega_0}\isdef \sqrt{k/m},\quad\mbox{and} \\ [10pt] r&=& \frac{x_0}{2} + j \frac{v_0}{2{\omega_0}} \;\isdef \; R_r e^{j\theta_r},\quad\hbox{with}\\ [10pt] R_r &\isdef & \frac{\sqrt{v^2_0 + {\omega_0}^2 x^2_0}}{2{\omega_0}}, \qquad \theta_r \;\isdef \; \tan^{-1}\left(\frac{v_0}{{\omega_0}x_0}\right) \end{eqnarray*}$$

denoting the modulus and angle of the pole residue $r$ , respectively. From §D.1, the inverse Laplace transform of $1/(s+a)$ is $e^{-at}u(t)$ , where $u(t)$ is the Heaviside unit step function at time 0 . Then by linearity, the solution for the motion of the mass is

$$\begin{eqnarray*} x(t) &=& re^{-j{\omega_0}t} + \overline{r}e^{j{\omega_0}t} = 2\mbox{re}\left\{re^{-j{\omega_0}t}\right\} = 2R_r\cos({\omega_0}t - \theta_r)\\ &=& \frac{\sqrt{v^2_0 + {\omega_0}^2 x^2_0}}{{\omega_0}} \cos\left[{\omega_0}t - \tan^{-1}\left(\frac{v_0}{{\omega_0}x_0}\right)\right]. \end{eqnarray*}$$

If the initial velocity is zero ($v_0=0$ ), the above formula reduces to $x(t) = x_0\cos({\omega_0}t)$ and the mass simply oscillates sinusoidally at frequency ${\omega_0}= \sqrt{k/m}$ , starting from its initial position $x_0$ . If instead the initial position is $x_0=0$ , we obtain

$$\begin{eqnarray*} x(t) &=& \frac{v_0}{{\omega_0}}\sin({\omega_0}t)\\ \;\Rightarrow\; v(t) &=& v_0\cos({\omega_0}t). \end{eqnarray*}$$