Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
A function 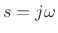 has a Laplace transform whenever it is of
exponential order. That is, there must be a real number
has a Laplace transform whenever it is of
exponential order. That is, there must be a real number 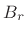 such that
such that
As an example, every exponential function
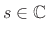 has a
Laplace transform for all finite values of
has a
Laplace transform for all finite values of 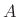 and
and 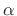 . Let's
look at this case more closely.
. Let's
look at this case more closely.
The Laplace transform of a causal, growing exponential function
is given by
Thus, the Laplace transform of an exponential
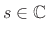 is
is
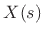 , but this is defined only for
re
, but this is defined only for
re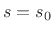 .
.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![$\displaystyle x(t) = \left\{\begin{array}{ll}
A e^{\alpha t}, & t\geq 0 \\ [5pt]
0, & t<0 \\
\end{array} \right.,
$](img1691.png)
![\begin{eqnarray*}
X(s) &\isdef & \int_0^\infty x(t) e^{-st}dt
= \int_0^\infty A e^{\alpha t} e^{-st}dt
= A \int_0^\infty e^{(\alpha - s) t} dt \\
&=& \left.\frac{A}{\alpha-s}e^{(\alpha - s) t} \right\vert _{0}^{\infty}
= \frac{A}{\alpha-s}e^{(\alpha - \sigma - j\omega) \infty}
- \frac{A}{\alpha-s}\\
&=& \left\{\begin{array}{ll}
\frac{A}{s-\alpha}, & \sigma>\alpha \\ [5pt]
\hbox{(indeterminate)}, & \sigma=\alpha \\ [5pt]
\infty, & \sigma<\alpha \\
\end{array} \right.
\end{eqnarray*}](img1692.png)
![]() is
is
![]() , but this is defined only for
re
, but this is defined only for
re![]() .
.