Ideal Mass

Figure 7.2: The ideal mass characterized by $f(t) = m \dot v(t) = m{\ddot x}(t)$ .

The concept of impedance extends also to masses and springs. Figure 7.2 illustrates an ideal mass of $m$ kilograms sliding on a frictionless surface. From Newton's second law of motion, we know force equals mass times acceleration, or

$$f(t) = m a(t) \isdef m \dot v(t) \isdef m \ddot x(t).$$

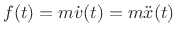
Since impedance is defined in terms of force and velocity, we will prefer the form $f(t) = m \dot v(t)$ . By the differentiation theorem for Laplace transforms [286],^8.1we have

$$F(s) = m [s V(s) - v(0)].$$

If we assume the initial velocity of the mass is zero, we have

$$F(s) = m s V(s),$$

and the impedance $F(s)/V(s)$ of the mass in the frequency domain is simply

$$R_m(s) \isdef m s.$$

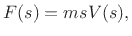
The admittance of a mass $m$ is therefore

$$\Gamma_m(s) \isdef \frac{1}{ms}$$

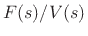
This is the transfer function of an integrator. Thus, an ideal mass integrates the applied force (divided by $m$ ) to produce the output velocity. This is just a ``linear systems'' way of saying force equals mass times acceleration.

Since we normally think of an applied force as an input and the resulting velocity as an output, the corresponding transfer function is $H(s) = \Gamma(s) = V(s)/F(s)$ . The system diagram for this view is shown in Fig. 7.3.

The impulse response of a mass, for a force input and velocity output, is defined as the inverse Laplace transform of the transfer function:

$$\gamma_m(t) \isdef {\cal L}^{-1}\left\{\Gamma_m(s)\right\} = \frac{1}{m}u(t)$$

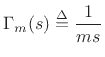
In this instance, setting the input to $\delta(t)$ corresponds to transferring a unit momentum to the mass at time 0 . (Recall that momentum is the integral of force with respect to time.) Since momentum is also equal to mass $m$ times its velocity $v(t)$ , it is clear that the unit-momentum velocity must be $v(t)=1/m$ .

Figure 7.3: Input/output description of a general impedance, with force $F(s)$ as the input, velocity $V(s)$ as the output, and admittance $\Gamma (s)$ as the transfer function.

Once the input and output signal are defined, a transfer function is defined, and therefore a frequency response is defined [488]. The frequency response is given by the transfer function evaluated on the $j\omega$ axis in the $s$ plane, i.e., for $s=j\omega$ . For the ideal mass, the force-to-velocity frequency response is

$$\Gamma_m(j\omega) = \frac{1}{m j\omega}$$

Again, this is just the frequency response of an integrator, and we can say that the amplitude response rolls off $-6$ dB per octave, and the phase shift is $-\pi /2$ radians at all frequencies.

In circuit theory, the element analogous to the mass is the inductor, characterized by $v(t) = L di/dt$ , or $V(s) = Ls I(s)$ . In an analog equivalent circuit, a mass can be represented using an inductor with value $L=m$ .