Let ![]() denote a function differentiable for all
denote a function differentiable for all ![]() such that
such that
![]() and the Fourier Transforms (FT) of both
and the Fourier Transforms (FT) of both ![]() and
and
![]() exist, where
exist, where
![]() denotes the time derivative
of
denotes the time derivative
of ![]() . Then we have
. Then we have
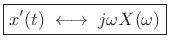
where
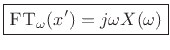
Proof:
This follows immediately from integration by parts:
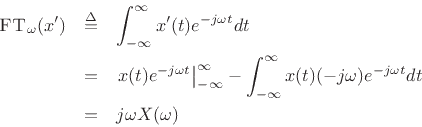
since
![]() .
.
The differentiation theorem is implicitly used in §E.6 to show that audio signals are perceptually equivalent to bandlimited signals which are infinitely differentiable for all time.