The scaling theorem (or similarity theorem) provides
that if you horizontally ``stretch'' a signal by the factor ![]() in the time domain, you ``squeeze'' its Fourier transform by the same
factor in the frequency domain. This is an important general Fourier
duality relationship.
in the time domain, you ``squeeze'' its Fourier transform by the same
factor in the frequency domain. This is an important general Fourier
duality relationship.
Theorem: For all continuous-time functions ![]() possessing a Fourier
transform,
possessing a Fourier
transform,
where
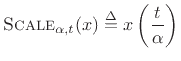
and
Proof:
Taking the Fourier transform of the stretched signals gives
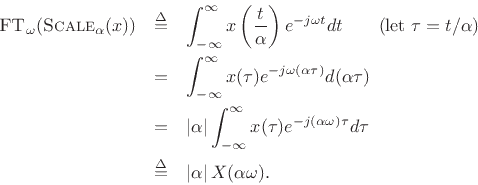
The absolute value appears above because, when ![]() ,
,
![]() , which brings out a minus sign in front of the
integral from
, which brings out a minus sign in front of the
integral from ![]() to
to ![]() .
.
The scaling theorem is fundamentally restricted to the
continuous-time, continuous-frequency (Fourier transform) case.
The closest we came to the scaling theorem among the DFT
theorems was the stretch theorem (§7.4.10). We found that
``stretching'' a discrete-time signal by the integer factor
![]() (filling in between samples with zeros) corresponded to the
spectrum being repeated
(filling in between samples with zeros) corresponded to the
spectrum being repeated ![]() times around the unit circle.
As a result, the ``baseband'' copy of the spectrum ``shrinks'' in
width (relative to
times around the unit circle.
As a result, the ``baseband'' copy of the spectrum ``shrinks'' in
width (relative to ![]() ) by the factor
) by the factor ![]() . Similarly,
stretching a signal using interpolation (instead of zero-fill)
corresponded to the same repeated spectrum with the spectral copies
zeroed out. The spectrum of the interpolated signal can therefore be
seen as having been stretched by the inverse of the time-domain
stretch factor. In summary, the stretch theorem for DFTs can be
viewed as the discrete-time, discrete-frequency counterpart of the
scaling theorem for Fourier Transforms.
. Similarly,
stretching a signal using interpolation (instead of zero-fill)
corresponded to the same repeated spectrum with the spectral copies
zeroed out. The spectrum of the interpolated signal can therefore be
seen as having been stretched by the inverse of the time-domain
stretch factor. In summary, the stretch theorem for DFTs can be
viewed as the discrete-time, discrete-frequency counterpart of the
scaling theorem for Fourier Transforms.