Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Filter-Bank Summation (FBS) Interpretation of the STFT
We can group the terms in the STFT definition differently to obtain
the filter-bank interpretation:
As will be explained further below (and illustrated further in
Figures 9.3, 9.4, and 9.5), under the filter-bank
interpretation, the spectrum of 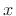 is first rotated along the
unit circle in the
is first rotated along the
unit circle in the 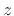 plane so as to shift frequency
plane so as to shift frequency  down
to 0
(via modulation by
down
to 0
(via modulation by
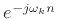 in the time domain), thus
forming the heterodyned signal
in the time domain), thus
forming the heterodyned signal
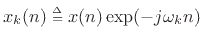 . Next, the heterodyned signal
. Next, the heterodyned signal 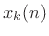 is lowpass-filtered to a
narrow band about frequency 0
(via convolving with the time-reversed
window
is lowpass-filtered to a
narrow band about frequency 0
(via convolving with the time-reversed
window
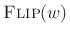 ). The STFT is thus interpreted as a
frequency-ordered collection of narrow-band time-domain
signals, as depicted in Fig.9.2. In other words, the STFT can be
seen as a uniform filter bank in which the input signal
). The STFT is thus interpreted as a
frequency-ordered collection of narrow-band time-domain
signals, as depicted in Fig.9.2. In other words, the STFT can be
seen as a uniform filter bank in which the input signal 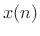 is converted to a set of
is converted to a set of  time-domain output signals
time-domain output signals
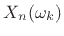 ,
,
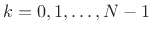 , one for each channel of the
, one for each channel of the
 -channel filter bank.
-channel filter bank.
Figure 9.2:
Filter Bank Summation (FBS) view of the STFT
 |
Expanding on the previous paragraph, the STFT (9.2) is
computed by the following operations:
The STFT output signal
 is regarded as a time-domain
signal (time index
is regarded as a time-domain
signal (time index 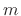 ) coming out of the
) coming out of the 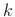 th channel of an
th channel of an
 -channel filter bank. The center frequency of the
-channel filter bank. The center frequency of the 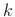 th channel
filter is
th channel
filter is
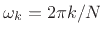 ,
,
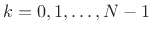 . Each channel
output signal is a baseband signal; that is, it is centered
about dc, with the ``carrier term''
. Each channel
output signal is a baseband signal; that is, it is centered
about dc, with the ``carrier term''
 taken
out by ``demodulation'' (frequency-shifting). In particular, the
taken
out by ``demodulation'' (frequency-shifting). In particular, the
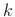 th channel signal is constant whenever the input signal happens to
be a sinusoid tuned to frequency
th channel signal is constant whenever the input signal happens to
be a sinusoid tuned to frequency  exactly.
exactly.
Note that the STFT analysis window 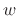 is now interpreted as (the flip
of) a lowpass-filter impulse response. Since the analysis window
is now interpreted as (the flip
of) a lowpass-filter impulse response. Since the analysis window 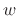 in the STFT is typically symmetric, we usually have
in the STFT is typically symmetric, we usually have
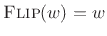 .
This filter is effectively frequency-shifted to provide each channel
bandpass filter. If the cut-off frequency of the window transform is
.
This filter is effectively frequency-shifted to provide each channel
bandpass filter. If the cut-off frequency of the window transform is
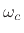 (typically half a main-lobe width), then each channel
signal can be downsampled significantly. This downsampling factor is
the FBS counterpart of the hop size
(typically half a main-lobe width), then each channel
signal can be downsampled significantly. This downsampling factor is
the FBS counterpart of the hop size 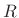 in the OLA context.
in the OLA context.
Figure 9.3 illustrates the filter-bank interpretation for  (the ``sliding STFT''). The input signal
(the ``sliding STFT''). The input signal 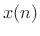 is frequency-shifted
by a different amount for each channel and lowpass filtered by the
(flipped) window.
is frequency-shifted
by a different amount for each channel and lowpass filtered by the
(flipped) window.
![\begin{psfrags}
% latex2html id marker 24346\psfrag{w}{\Large$\protect\hbox{\sc Flip}(w)$}\psfrag{x(n)}{\LARGE$x(n)$}\psfrag{X0}{\LARGE$X_n(\omega_{\scriptscriptstyle 0}$)}\psfrag{X1}{\LARGE$X_n(\omega_{\scriptscriptstyle 1}$)}\psfrag{XNm1}{\LARGE$X_n(\omega_{\scriptscriptstyle {N}-1})$}\psfrag{ejw0}{\huge$e^{-j\omega_{\scriptscriptstyle 0}n}$}\psfrag{ejw1}{\huge$e^{-j\omega_{\scriptscriptstyle 1}n}$}\psfrag{ejwNm1}{\huge$e^{-j\omega_{\scriptscriptstyle {N-1}}n}$}\psfrag{dR}{\LARGE$\downarrow R$}\psfrag{X}{\LARGE$\times$}\begin{figure}[htbp]
\includegraphics[width=3in]{eps/fbs1}
\caption{Sliding STFT analysis filter bank.
The $k$th channel of the filter bank computes
$X_n(\omega_k)=(x_k\ast \hbox{\sc Flip}{w})(n)$, where $x_k(n)\isdeftext
x(n)\exp(-j\omega_k n)$.
}
\end{figure}
\end{psfrags}](img1544.png)
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![$\displaystyle \sum_{n=-\infty}^\infty \underbrace{[ x(n)e^{-j\omega_k n}]}_{x_k(n)} w(n-m)$](img1530.png)
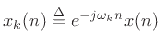 .
.
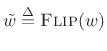 to get
to get
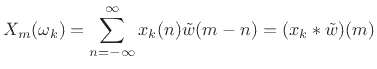
![]() is now interpreted as (the flip
of) a lowpass-filter impulse response. Since the analysis window
is now interpreted as (the flip
of) a lowpass-filter impulse response. Since the analysis window ![]() in the STFT is typically symmetric, we usually have
in the STFT is typically symmetric, we usually have
![]() .
This filter is effectively frequency-shifted to provide each channel
bandpass filter. If the cut-off frequency of the window transform is
.
This filter is effectively frequency-shifted to provide each channel
bandpass filter. If the cut-off frequency of the window transform is
![]() (typically half a main-lobe width), then each channel
signal can be downsampled significantly. This downsampling factor is
the FBS counterpart of the hop size
(typically half a main-lobe width), then each channel
signal can be downsampled significantly. This downsampling factor is
the FBS counterpart of the hop size ![]() in the OLA context.
in the OLA context.
![]() (the ``sliding STFT''). The input signal
(the ``sliding STFT''). The input signal ![]() is frequency-shifted
by a different amount for each channel and lowpass filtered by the
(flipped) window.
is frequency-shifted
by a different amount for each channel and lowpass filtered by the
(flipped) window.