STFT Filter Bank

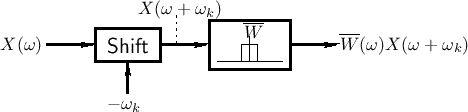
Each channel of an STFT filter bank implements the processing shown in Fig.9.4. The same processing is shown in the frequency domain in Fig.9.5. Note that the window transform $W(\omega)$ is complex-conjugated because the window $w$ is flipped in the time domain, i.e., $w(-n)\;\leftrightarrow\;\overline{W(\omega)}$ when $w$ is real [264].

Figure: One channel of the STFT filter bank computing $X_n(\omega _k)=(x_k\ast {\tilde w})(n)$ , where $x_k(n)\isdeftext x(n)\exp(-j\omega_k n)$ , and ${\tilde w}\isdeftext \hbox{\sc Flip}(w)$ .

Figure: One channel of the STFT filter bank in the frequency domain ( $\overline {W}$ denotes the complex conjugate of $W$ ).

These channels are then arranged in parallel to form a filter bank, as shown in Fig.9.3. In practice, we need to know under what conditions the channel filters $w$ will yield perfect reconstruction when the channel signals are remodulated and summed. (A sufficient condition for the sliding STFT is that the channel frequency responses overlap-add to a constant over the unit circle in the frequency domain.) Furthermore, since the channel signals are heavily oversampled, particularly when the chosen window $w$ has low side-lobe levels, we would like to be able to downsample the channel signals without loss of information. It is indeed possible to downsample the channel signals while retaining the perfect reconstruction property, as we will see in §9.8.1.