Maximum Phase Filters

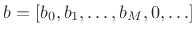
The opposite of minimum phase is maximum phase:

$\parbox{0.8\textwidth}{% A stable LTI filter $H(z)=B(z)/A(z)$\ is said to be \emph{maximum phase} if all its zeros are outside the unit circle.}$

For example, every stable allpass filter (§B.2) is a maximum-phase filter, because its transfer function can be written as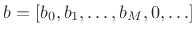

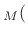
$$H(z)=\frac{z^{-N}A(z^{-1})}{A(z)},$$

where $A(z)=1+a_1z^{-1}+a_2z^{-2}+\cdots+a_N z^{-N}$ is an $N$ th-order minimum-phase polynomial in $z^{-1}$ (all roots inside the unit circle). As another example of a maximum-phase filter (a special case of allpass filters, in fact), a pure delay of $N$ samples has the transfer function $z^{-N}$ , which is $N$ poles at $z=0$ and $N$ zeros at $z=\infty$ .

If zeros of $B(z)$ occur both inside and outside the unit circle, the filter is said to be a mixed-phase filter. Note that zeros on the unit circle are neither minimum nor maximum phase according to our definitions. Since poles on the unit circle are sometimes called ``marginally stable,'' we could say that zeros on the unit circle are ``marginally minimum and/or maximum phase'' for consistency. However, such a term does not appear to be very useful. When pursuing minimum-phase filter design (see §11.7), we will find that zeros on the unit circle must be treated separately.

If $B(z)$ is order $M$ and minimum phase, then $z^{-M}B(z^{-1})$ is maximum phase, and vice versa. To restate this in the time domain, if $b=[b_0,b_1,\ldots,b_M,0,\ldots]$ is a minimum-phase FIR sequence of length $M+1$ , then SHIFT$_M($FLIP$(b))$ is a maximum-phase sequence. In other words, time reversal inverts the locations of all zeros, thereby ``reflecting'' them across the unit circle in a manner that does not affect spectral magnitude. Time reversal is followed by a shift in order to obtain a causal result, but this is not required: Adding a pure delay to a maximum-phase filter ( $B(z) \to z^{-1}B(z)$ ) gives a new maximum-phase filter with the same amplitude response (and order increased by 1).