A filter is minimum phase if both the numerator and denominator of its
transfer function are
minimum-phase polynomials
in ![]() :
:
The case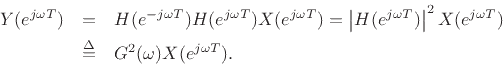
As usual, definitions for filters generalize to definitions for signals by simply treating the signal as an impulse response:
Note that every stable all-pole filter
![]() is
minimum phase, because stability implies that
is
minimum phase, because stability implies that ![]() is minimum
phase, and there are ``no zeros'' (all are at
is minimum
phase, and there are ``no zeros'' (all are at ![]() ).
Thus, minimum phase is the only phase available to a stable all-pole
filter.
).
Thus, minimum phase is the only phase available to a stable all-pole
filter.
The contribution of minimum-phase zeros to the complex cepstrum was described in §8.8.