Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
It is easy to classify completely all first-order FIR filters:
where we have normalized  to 1 for simplicity. We have a single
zero at
to 1 for simplicity. We have a single
zero at 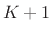 . If
. If
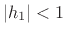 , the filter is minimum phase. If
, the filter is minimum phase. If
 , it is maximum phase. Note that the minimum-phase case
is the one in which the impulse response
, it is maximum phase. Note that the minimum-phase case
is the one in which the impulse response
![$ [1,h_1,0,\ldots]$](img1270.png) decays instead of grows. It can be shown that this is a general
property of minimum-phase sequences, as elaborated in the next
section.
decays instead of grows. It can be shown that this is a general
property of minimum-phase sequences, as elaborated in the next
section.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]