Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
The previous example is an instance of the following general result:

That is, the signal energy in the first 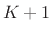 samples of the
minimum-phase case is at least as large as any other causal signal
having the same magnitude spectrum. (See [60]
for a proof outline.) Thus, minimum-phase signals are maximally
concentrated toward time 0 when compared against all causal signals
having the same magnitude spectrum. As a result of this property,
minimum-phase signals are sometimes called minimum-delay
signals.
samples of the
minimum-phase case is at least as large as any other causal signal
having the same magnitude spectrum. (See [60]
for a proof outline.) Thus, minimum-phase signals are maximally
concentrated toward time 0 when compared against all causal signals
having the same magnitude spectrum. As a result of this property,
minimum-phase signals are sometimes called minimum-delay
signals.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]

