Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Let
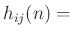 impulse response from source
impulse response from source 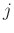 to ear
to ear 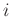 .
Then the output is given by six convolutions:
.
Then the output is given by six convolutions:
Transfer-function matrix:
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download Reverb.pdf
Download Reverb_2up.pdf
Download Reverb_4up.pdf
![]() impulse response from source
impulse response from source ![]() to ear
to ear ![]() .
Then the output is given by six convolutions:
.
Then the output is given by six convolutions:
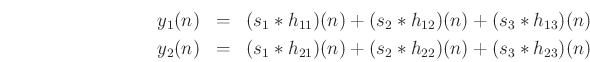
![$\displaystyle \left[\begin{array}{c} Y_1(z) \\ [2pt] Y_2(z) \end{array}\right] =
\left[\begin{array}{ccc}
H_{11}(z) & H_{12}(z) & H_{13}(z)\\ [5pt]
H_{21}(z) & H_{22}(z) & H_{23}(z)
\end{array}\right]
\left[\begin{array}{c} S_1(z) \\ [2pt] S_2(z) \\ [2pt] S_3(z)\end{array}\right]
$](img8.png)