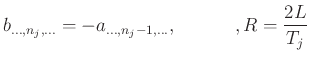Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
MD N-ports
Need to extend the notion of passivity to distributed networks.
Basic element, the  -port has the same form in multi-D:
-port has the same form in multi-D:
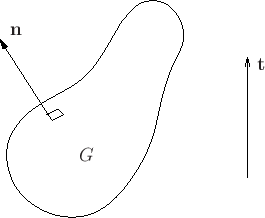
- ``Port'' is no longer localized in space, and thus we have, for any port
 ,
,
- instantaneous power (or power density) absorbed at any point
 is
is
- Also have distributed source power
 and dissipated power
and dissipated power 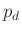
 -ports must be connected portwise
-ports must be connected portwise
- stored energy requires a generalized treatment...
MD N-ports Continued
MD-Passivity
An MD  -port is called integrally
-port is called integrally 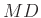 -passive (in
-passive (in 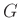 ) if we have
) if we have
or differentially 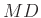 passive, if we have
passive, if we have
and 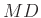 -lossless if equality holds.
-lossless if equality holds.
The MD Inductor
Consider the following relation:
where 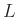 is a positive constant, and
is a positive constant, and
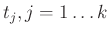 is an causal coordinate.
is an causal coordinate.
- Defined over entire
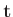 space, but is really just a set of
space, but is really just a set of 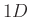 differential relations.
differential relations.
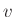 obtained from
obtained from 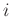 by integrating in
by integrating in 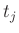 direction (forward in time).
direction (forward in time).
We can define a discrete approximation by applying the trapezoid rule in the 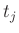 direction:
direction:
And introducing wave variables,
can get the MD-equivalent of the wave-digital inductance one-port:
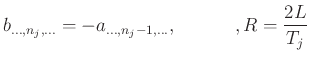 |
(1) |
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download Meshes.pdf
Download Meshes_2up.pdf
Download Meshes_4up.pdf
![]() -port has the same form in multi-D:
-port has the same form in multi-D:
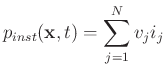
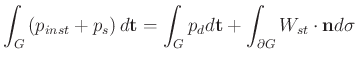
![]() -port is called integrally
-port is called integrally ![]() -passive (in
-passive (in ![]() ) if we have
) if we have
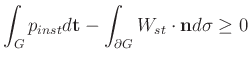
![]() direction:
direction: