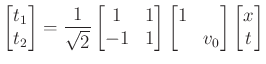Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Symmetric Hyperbolic Systems
Multidimensional time and space-dependent physical systems are often described by systems of PDEs which are symmetric hyperbolic. For example, in 1D, a typical situation is:
where
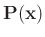 is symmetric,
is symmetric, 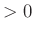 , and
, and
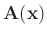 is symmetric (both square, real). Can write:
is symmetric (both square, real). Can write:
and integrating over the real line (assuming no boundaries,
-
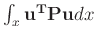 is usually called the total energy of the system.
is usually called the total energy of the system.
- like an ODE describing evolution of energy.
- if right-hand side is zero, then the system is lossless (in weighted
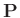 norm).
norm).
- if right-hand side is never positive, then the energy can only decrease.
- symmetric hyperbolic
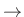 reciprocal networks (almost).
reciprocal networks (almost).
CFL Criterion
Hyperbolic systems
 finite propagation speeds.
finite propagation speeds.
For explicit numerical methods on a grid, have a necessary stability condition on the time-step space-step ratio. In 1D, on a regular grid, only neighboring points:
(Courant-Friedrichs-Lewy Condition).
In higher-D, same general result, but extra factors appear (solution does not necessarily move along a grid direction).
In the network approaches, CFL appears in an elementary way as a constraint on the positivity of the circuit elements (for passivity).
Multidimensional Problems and Coordinate Transformation
Multidimensional (distributed) systems
 system of PDEs.
system of PDEs.
Time-dependent systems derived from conservation laws:
- may be of hyperbolic type (finite speeds)
- quantities conserved with respect to time alone.
In order to obtain a multidimensional circuit representation of a system of PDEs, useful to consider coordinate changes
New coordinates should be causal, in the sense that:
- Any positive change
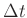 in the variable
in the variable 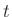 (time) must be reflected by a similar positive change
(time) must be reflected by a similar positive change
 in all the new coordinates
in all the new coordinates 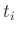 ,
,
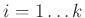 .
.
- Conversely, any positive change
 in any of the new coordinates must produce a positive change in the time variable
in any of the new coordinates must produce a positive change in the time variable 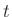 .
.
A simple set of linear coordinate transformations:
Remarks: A theoretical ``hack'' for extending passivity ideas to multi-D
A Simple Coordinate Change and Sampling
If we have only one spatial dimension, then coordinate change options are limited. The only suitable one (in this context) is
A simple rotation of the coordinates by 45 degrees. If we now define uniform grids in the two coordinate systems, we get:
- grid spacings
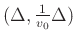 in original coordinates,
in original coordinates,
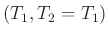 in new.
in new.
- grids partially align, if we have
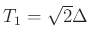 .
.
Coordinate Changes in Higher Dimensions: Hexagonal Coordinates
The transformation defined by
when uniformly ``sampled'' in the new coordinates gives rise to the following grid pattern (viewed in the original coordinate system):
Three different grids (white, grey, black points) which exist every third time step.
Rectangular coordinates
In order to generate a standard rectangular grid by uniformly sampling in the causal coordinates, need to use an embedding:
which maps 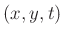 to a 5-dimensional space
to a 5-dimensional space 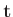 = (north+time , south+time , east+time, west+time, time alone), and we get a normal rectangular grid in
= (north+time , south+time , east+time, west+time, time alone), and we get a normal rectangular grid in 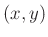 if we sample uniformly in the five directions
if we sample uniformly in the five directions
- Ugly theoretical manipulation to do something simple; not actually going to solve a problem in 5D. Need them to define directions of energy flow.
- Now need to define a particular right pseudo-inverse
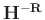 ...in practice, choice is relatively immaterial (but still must have elements of right column positive).
...in practice, choice is relatively immaterial (but still must have elements of right column positive).
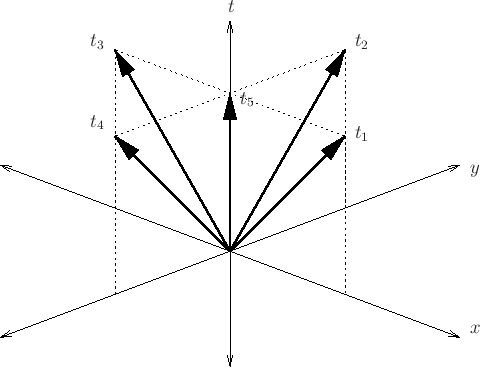
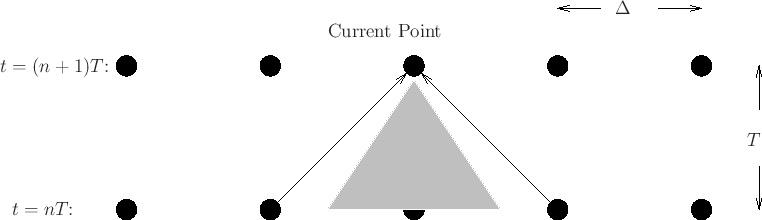
- Crux is: need five dimensions for a rectilinear grid, because in a simulation, energy can approach a grid point from any of the four compass points (and also from a past grid point at the same location).
- in 3D need to embed in a 7-D system.
Picture is:
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download Meshes.pdf
Download Meshes_2up.pdf
Download Meshes_4up.pdf
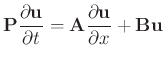
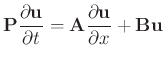
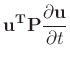
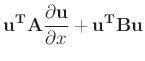
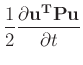
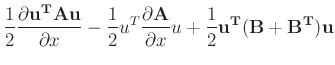

![]() finite propagation speeds.
finite propagation speeds.
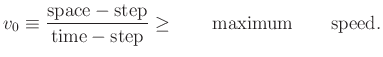
![]() system of PDEs.
system of PDEs.