


Next: Wave Digital Elements
Up: Wave Digital Elements and
Previous: Wave Variables
Fettweis [42] defines the instantaneous pseudopower absorbed by a port with port resistance 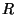 (real) at time step
(real) at time step  in terms of the discrete input and output wave quantities as
in terms of the discrete input and output wave quantities as
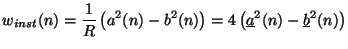 |
(2.18) |
which, when the transformation (2.14) is inverted, gives
This discrete power definition coincides with the standard definition of power in classical network theory from (2.2), aside from the factor of 4, which is of no consequence if definition (2.18) is applied consistently throughout a wave digital network.
For a real LTI  -port, in an exponential state of complex frequency
-port, in an exponential state of complex frequency 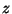 , the steady-state average pseudopower may be written in terms of the
, the steady-state average pseudopower may be written in terms of the 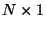 vectors
vectors
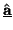 and
and
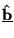 which contain the power-normalized complex amplitudes
which contain the power-normalized complex amplitudes
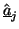 and
and
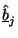 , for
, for
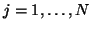 as
as
The steady-state reflectance
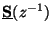 is defined by
is defined by
and gives
where
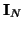 is the
is the 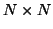 identity matrix. For pseudopassivity [42], we require, then (recalling that the bilinear transform (2.11) maps the right half
identity matrix. For pseudopassivity [42], we require, then (recalling that the bilinear transform (2.11) maps the right half 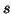 -plane to the exterior of the unit circle in the
-plane to the exterior of the unit circle in the 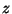 plane) that
plane) that
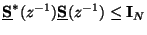 for for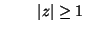 |
(2.19) |
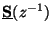 is sometimes called a bounded real matrix. If (2.19) holds with equality for
is sometimes called a bounded real matrix. If (2.19) holds with equality for 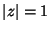 , then it is called lossless bounded real (LBR) [193]. In general, to bounded real matrix reflectances there correspond positive real matrix impedances, and vice versa. In terms of voltage wave quantities, we have for a wave digital
, then it is called lossless bounded real (LBR) [193]. In general, to bounded real matrix reflectances there correspond positive real matrix impedances, and vice versa. In terms of voltage wave quantities, we have for a wave digital  -port, that
-port, that
where
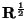 is the diagonal square root of the matrix containing the
is the diagonal square root of the matrix containing the  port resistances
port resistances
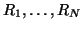 on its diagonal. We then have
on its diagonal. We then have
for the voltage wave scattering matrix 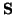 and thus we require
and thus we require
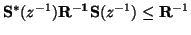 for for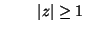 |
(2.20) |
for passivity. For one-ports, the requirements (2.20) and (2.19) are the same.
Also note that we have, by applying the power wave variable definitions (2.16), and the discrete impedance relation
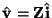 (which is identical to the analog relation from (2.1), except that we now have
(which is identical to the analog relation from (2.1), except that we now have
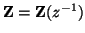 ), that
), that
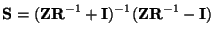 |
(2.21) |
If the  -port is not LTI, then it is possible to apply a similar idea to the expression for the instantaneous pseudopower, from (2.18) in order to derive a passivity condition [46]; In this case, pseudopassivity has also been called incremental pseudopassivity [125].
-port is not LTI, then it is possible to apply a similar idea to the expression for the instantaneous pseudopower, from (2.18) in order to derive a passivity condition [46]; In this case, pseudopassivity has also been called incremental pseudopassivity [125].



Next: Wave Digital Elements
Up: Wave Digital Elements and
Previous: Wave Variables
Stefan Bilbao
2002-01-22
![]() (real) at time step
(real) at time step ![]() in terms of the discrete input and output wave quantities as
in terms of the discrete input and output wave quantities as
![]() -port, in an exponential state of complex frequency
-port, in an exponential state of complex frequency ![]() , the steady-state average pseudopower may be written in terms of the
, the steady-state average pseudopower may be written in terms of the ![]() vectors
vectors
![]() and
and
![]() which contain the power-normalized complex amplitudes
which contain the power-normalized complex amplitudes
![]() and
and
![]() , for
, for
![]() as
as
![]() (which is identical to the analog relation from (2.1), except that we now have
(which is identical to the analog relation from (2.1), except that we now have
![]() ), that
), that
![]() -port is not LTI, then it is possible to apply a similar idea to the expression for the instantaneous pseudopower, from (2.18) in order to derive a passivity condition [46]; In this case, pseudopassivity has also been called incremental pseudopassivity [125].
-port is not LTI, then it is possible to apply a similar idea to the expression for the instantaneous pseudopower, from (2.18) in order to derive a passivity condition [46]; In this case, pseudopassivity has also been called incremental pseudopassivity [125].