


Next: Kirchoff's Laws
Up: Classical Network Theory
Previous: N-ports
Power and Passivity
The total instantaneous power absorbed by a real  -port is defined by
-port is defined by
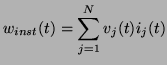 |
(2.2) |
where 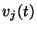 and
and 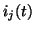 are the real instantaneous voltage and current at port
are the real instantaneous voltage and current at port 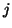 .
In general, for an
.
In general, for an  -port which contains stored energy
-port which contains stored energy 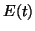 , which dissipates energy at rate
, which dissipates energy at rate 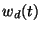 , and which contains sources which provide energy at rate
, and which contains sources which provide energy at rate 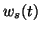 , then the energy balance
, then the energy balance
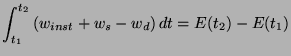 |
(2.3) |
must hold over any interval
![$ [t_{1},t_{2}]$](img217.png) . Such an
. Such an  -port is called passive if we have
-port is called passive if we have
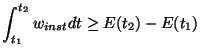 |
(2.4) |
over any time interval; the increase in stored energy must be less than the energy delivered through the ports. The  -port is called lossless if (2.4) holds with equality over any interval.
-port is called lossless if (2.4) holds with equality over any interval.
For a linear time-invariant  -port, in an exponential state of complex frequency
-port, in an exponential state of complex frequency 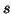 , we can define the total complex power absorbed to be the inner product
, we can define the total complex power absorbed to be the inner product
and the average or active power as
where 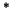 denotes transpose conjugation. For an
denotes transpose conjugation. For an  -port defined by an impedance relationship, we may immediately write, in terms of the voltage and current amplitudes,
-port defined by an impedance relationship, we may immediately write, in terms of the voltage and current amplitudes,
For such a real LTI  -port, passivity may be defined in the following way. If the total active power absorbed by an
-port, passivity may be defined in the following way. If the total active power absorbed by an  -port is always greater than or equal to zero for frequencies
-port is always greater than or equal to zero for frequencies 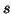 such that Re
such that Re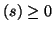 , then it is called passive. This implies that
, then it is called passive. This implies that
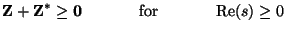 |
(2.5) |
A matrix Z with such a property is called a positive matrix. In the present case of a real  -port,
-port,  is called positive real (though in general, positivity is all that is required for passivity).
If the average power absorbed is identically zero for Re
is called positive real (though in general, positivity is all that is required for passivity).
If the average power absorbed is identically zero for Re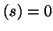 , or, in terms of impedances, if
, or, in terms of impedances, if
then the  -port is called lossless.
-port is called lossless.



Next: Kirchoff's Laws
Up: Classical Network Theory
Previous: N-ports
Stefan Bilbao
2002-01-22
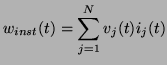
![]() -port, in an exponential state of complex frequency
-port, in an exponential state of complex frequency ![]() , we can define the total complex power absorbed to be the inner product
, we can define the total complex power absorbed to be the inner product
![]() -port, passivity may be defined in the following way. If the total active power absorbed by an
-port, passivity may be defined in the following way. If the total active power absorbed by an ![]() -port is always greater than or equal to zero for frequencies
-port is always greater than or equal to zero for frequencies ![]() such that Re
such that Re![]() , then it is called passive. This implies that
, then it is called passive. This implies that