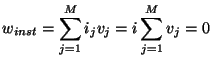Next: Circuit Elements
Up: Classical Network Theory
Previous: Power and Passivity
Kirchoff's Laws
Connections between individual ports can be made through an appeal to Kirchoff's Laws, which specify two important connection rules. Kirchoff's Voltage Law (KVL) states that for a series connection, as pictured in Figure 2.2(a), the currents will be equal in all ports to be connected, and that the sum of the voltages at all ports is zero, or, in other words, if we have a series connection of  ports,
ports,
Kirchoff's Current Law (KCL) specifies the dual relationship among the voltages and currents in the case of a parallel connection of  ports, as per Figure 2.2(b), as
ports, as per Figure 2.2(b), as
Figure 2.2:
Kirchoff connections of  ports, in (a) series and (b) parallel.
ports, in (a) series and (b) parallel.
 |
Both sets of constraints hold instantaneously and can be thought of as  -ports in their own right. In addition, both types of
-ports in their own right. In addition, both types of  -port are passive, and in fact lossless. For example, in the case of a series connection of
-port are passive, and in fact lossless. For example, in the case of a series connection of  ports where the currents at every port are the same and equal to
ports where the currents at every port are the same and equal to  , we have, from (2.2), that
, we have, from (2.2), that
Losslessness of the parallel connection can be similarly demonstrated. It is possible to show, through the use of Tellegen's Theorem [136] that a network made up of Kirchoff connections of passive  -ports will behave passively as a whole.
-ports will behave passively as a whole.



Next: Circuit Elements
Up: Classical Network Theory
Previous: Power and Passivity
Stefan Bilbao
2002-01-22
![]() -ports in their own right. In addition, both types of
-ports in their own right. In addition, both types of ![]() -port are passive, and in fact lossless. For example, in the case of a series connection of
-port are passive, and in fact lossless. For example, in the case of a series connection of ![]() ports where the currents at every port are the same and equal to
ports where the currents at every port are the same and equal to ![]() , we have, from (2.2), that
, we have, from (2.2), that