An Alternate MDKC and Scattering Network

The use of network manipulations and alternate spectral mappings in order to derive digital waveguide networks from an MDKC has been discussed in detail in §4.10, and we have seen the idea applied again in Chapter 5 to beam and plate systems. This same idea can be employed in the present case as well. Consider the network of Figure B.3(a), which is equivalent to that of Figure B.2(a); the right-hand pair of inductors in series in the ``pressure'' loop has been replaced by a gyrator closed on a parallel combination of capacitors; notice that although we are now transforming nonlinear operators, the network transformation techniques are no different from the linear case. We thus have a powerful means of developing stable numerical methods at our disposal.

The element values $L_{11}$, $L_{22}$, $M_{11}$ and $M_{22}$ are the same as before, except scaled by a factor $\Delta$, and the capacitance value will be

$$C_{33} = L_{33}\Delta/2\hspace{0.5in}F_{33} = M_{33}\Delta/2$$

where $L_{33}$ and $M_{33}$ are as defined in Figure B.2. (Notice that we have scaled the entire system by $\Delta$, as in §4.10.)

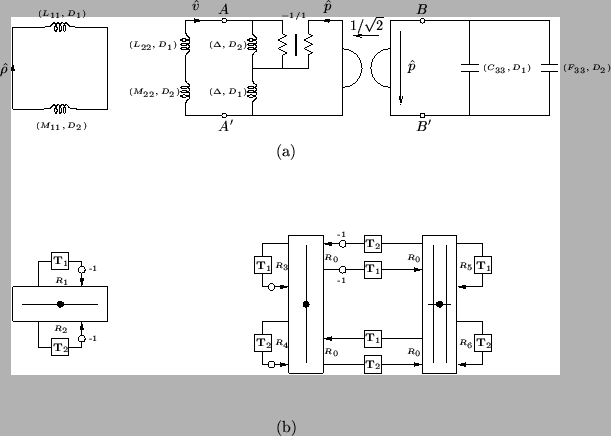
The resulting MD digital network is shown in Figure B.3(b). As before, the two-port $AABB'$ transforms to a pair of bidirectional delay lines under the application of the spectral mappings defined by (4.107). The other circuit elements, namely the nonlinear inductors and capacitors, must be discretized using the trapezoid rule, and so we are left with a network which is neither an MDWDF nor a DWN, but which contains elements of both. The port resistance are determined in the usual way; for an inductance $L$ and direction $t_{j}$, by $R=2L/T_{j}$ and for a capacitance $C$ of direction $t_{j}$ by $R = T_{j}/(2C)$. The port resistances of the paired multidimensional unit elements will be $R_{0} = 1/\sqrt{2}$.

Figure B.3: Alternative networks for the (1+1)D gas dynamics system-- (a) MDKC and (b) scattering network.

It would be possible to choose the directional shift lengths in the one-port inductances and capacitances differently from those in the unit elements such that the network could conceivably operate in an interleaved (offset) configuration; parallel junctions which calculate $p$ alternate with series junctions calculating $v$. A potential problem here is that the port resistances at the parallel junctions (say) depend on $v$, but $v$ are not calculated at these grid locations; some approximation is thus necessary, but we do not pursue the matter further here.