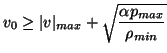Next: An Alternate MDKC and
Up: The Gas Dynamics Equations
Previous: The Gas Dynamics Equations
It is particularly easy to see the form of the MDKC for the gas dynamics equations in the scaled form of (B.13). Applying the usual coordinate transformation (3.18), (B.13) becomes
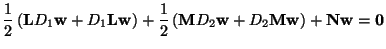 |
(B.16) |
with
and
The MDKC is shown in Figure B.2(a), where the inductances can be read directly from the entries of 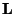 ,
, 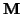 and
and 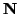 .
. 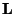 and
and 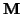 represent the inductances in the three loops in directions
represent the inductances in the three loops in directions 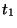 and
and 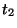 respectively, and
respectively, and 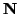 gives the coupling between the second and third loops (notice that it can be realized as a simple linear and shift-invariant Jaumann two-port, just as in the linear systems of Chapter 3). The first loop, with current
gives the coupling between the second and third loops (notice that it can be realized as a simple linear and shift-invariant Jaumann two-port, just as in the linear systems of Chapter 3). The first loop, with current
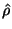 is decoupled from the other two, although the inductances in this loop are dependent on
is decoupled from the other two, although the inductances in this loop are dependent on 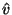 .
.
The MDWD network follows immediately, and is shown in Figure B.2(b). It should be kept in mind that the port resistances at the adaptors are now functions of the dependent variables (the currents in the MDKC), and thus of the wave variables themselves. In a given updating cycle, the current values of the port resistances must be determined from the incoming waves. Due to the fact that power normalized variables are used, this leads to a system of coupled nonlinear algebraic equations (three, one for each adaptor) to be solved at every grid point, and at every time step.
Figure B.2:
The (1+1)D gas dynamics system-- (a) MDKC and (b) MDWD-network.
|
|
Passivity is contingent upon the positivity of all the inductances in the network; this is essentially a condition on the positivity of the diagonal matrices 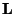 and
and 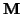 . Proceeding down the diagonals, this requirement on the first elements leads to the natural condition
. Proceeding down the diagonals, this requirement on the first elements leads to the natural condition
where 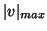 is the maximum value that
is the maximum value that 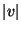 will take over the problem domain, and during the simulation period. We have also assumed that
will take over the problem domain, and during the simulation period. We have also assumed that 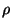 remains positive, and used the definition of the scaled quantity
remains positive, and used the definition of the scaled quantity 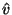 from (B.11). The conditions on the other elements of
from (B.11). The conditions on the other elements of 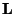 and
and 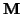 are more strict. We get
are more strict. We get
where
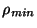 and
and 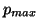 are, respectively, the minimal value of
are, respectively, the minimal value of 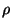 and the maximum value of
and the maximum value of 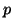 that will be encountered in the problem space. These quantities, as well as
that will be encountered in the problem space. These quantities, as well as 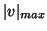 must be estimated a priori. It is also worth mentioning that for the above reasoning to be valid, it has been assumed that
must be estimated a priori. It is also worth mentioning that for the above reasoning to be valid, it has been assumed that 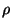 and
and 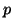 will remain positive, and that
will remain positive, and that 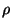 is bounded from below. Although this has not been mentioned in the literature, there does not appear to be any assurance that these assumptions will remain valid during the course of a simulation.
is bounded from below. Although this has not been mentioned in the literature, there does not appear to be any assurance that these assumptions will remain valid during the course of a simulation.
We still have one degree of freedom left, namely the value of the parameter 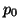 . An optimal setting is easily shown to be
. An optimal setting is easily shown to be
in which case the two bounds on 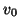 from (B.17) coalesce, giving
from (B.17) coalesce, giving



Next: An Alternate MDKC and
Up: The Gas Dynamics Equations
Previous: The Gas Dynamics Equations
Stefan Bilbao
2002-01-22
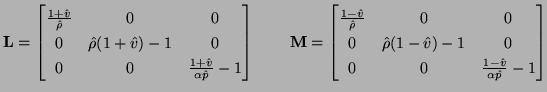
![]() . An optimal setting is easily shown to be
. An optimal setting is easily shown to be