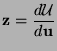Next: An open problem
Up: The Gas Dynamics Equations
Previous: An Alternate MDKC and
Entropy Variables
In §B.3, we showed how Fettweis et al. have effectively employed a skew-selfadjoint form of the gas dynamics system in order to generate a circuit model. Such forms have been the subject of a great deal of research, especially in the last few years [181]. One particular form, which makes use of so-called entropy variables would appear to be of fundamental importance, because it arises from a change of variables (and not a simple scaling of the system, as was the case for the system arrived at in §B.3). We recap the results from [181] here.
Consider a system of conservation laws,
 |
(B.18) |
where the
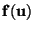 are smooth, possibly nonlinear mappings. The gas dynamics system (B.9), with
are smooth, possibly nonlinear mappings. The gas dynamics system (B.9), with
![$ {\bf u} = [\rho, \rho v, \rho e]^{T}$](img3195.png) and
and
![$ {\bf f}({\bf u}) = [\rho v, \rho v^{2} +p, \rho v e +pv]^{T}$](img3196.png) , again complemented by the constitutive relation (B.10) is of this form. It is noted in [68,116,182] that (B.18) implies a further conservation law,
, again complemented by the constitutive relation (B.10) is of this form. It is noted in [68,116,182] that (B.18) implies a further conservation law,
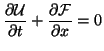 |
(B.19) |
for some smooth convex scalar function
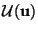 , and a scalar flux
, and a scalar flux
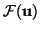 , over any time interval over which solutions to (B.18) remain smooth. If discontinuities (shocks) develop, then (B.19) becomes an inequality (
, over any time interval over which solutions to (B.18) remain smooth. If discontinuities (shocks) develop, then (B.19) becomes an inequality (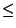 ).
).
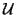 and
and
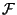 are related by
are related by
It was shown in [183] that system (B.18) is symmetrized through left-multiplication by the Hessian
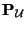 of
of
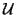 ,
,
so that we have
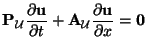 |
(B.20) |
where
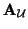 and
and
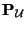 are symmetric, and in addition
are symmetric, and in addition
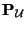 is positive definite (a result of the convexity requirement on
is positive definite (a result of the convexity requirement on
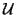 ). This nonlinear system is of the same form as the (linear) symmetric hyperbolic system (3.1) discussed in §3.2, and possesses many similar properties; this form, however, can not be easily approached through MD circuit methods. Furthermore, weak solutions (i.e. solutions involving discontinuities) will not be preserved under such a scaling [181]. This is the same defect as that of Fettweis's MDKC for the Euler system, as discussed in §B.3.
). This nonlinear system is of the same form as the (linear) symmetric hyperbolic system (3.1) discussed in §3.2, and possesses many similar properties; this form, however, can not be easily approached through MD circuit methods. Furthermore, weak solutions (i.e. solutions involving discontinuities) will not be preserved under such a scaling [181]. This is the same defect as that of Fettweis's MDKC for the Euler system, as discussed in §B.3.
It was later shown that (B.18) can also symmetrized with respect to a new variable 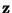 , defined by
, defined by
In this case, symmetrization is carried out through a variable change and not a scaling, so weak solutions are indeed preserved. If, furthermore, the flux 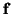 is homogeneous [181], it can be shown that there is also a skew-selfadjoint form of (B.18). The gas dynamics system (B.9) can be written in skew-selfadjoint form as
is homogeneous [181], it can be shown that there is also a skew-selfadjoint form of (B.18). The gas dynamics system (B.9) can be written in skew-selfadjoint form as
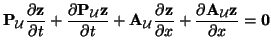 |
(B.21) |
if
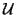 is chosen as
is chosen as
which is closely related to the physical entropy of the system [181]. The new variables 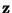 are referred to as entropy variables.
are referred to as entropy variables.
Subsections



Next: An open problem
Up: The Gas Dynamics Equations
Previous: An Alternate MDKC and
Stefan Bilbao
2002-01-22

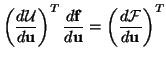
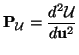
![]() , defined by
, defined by