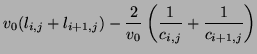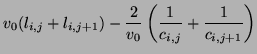Type I: Voltage-centered Mesh

At a parallel junction, we set the self-loop admittance 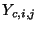$Y_{c,i,j}$ to zero, and the admittances of the branches leading away from a parallel junction at grid point 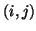$(i,j)$ to be identical, thus

$$Y_{c,i,j} = 0\hspace{1,0in}Y_{x^{-},i,j} = Y_{x^{+},i,j} = Y_{y^{-},i,j} = Y_{y^{+},i,j} = \frac{v_{0}}{2}c_{i,j}$$

and set

$$Z_{c,i+\frac{1}{2},j} = v_{0}(l_{i,j}+l_{i+1,j})-\frac{2}{v_{0}}\left(\frac{1}{c_{i,j}}+\frac{1}{c_{i+1,j}}\right)$$

$$Z_{c,i,j+\frac{1}{2}} = v_{0}(l_{i,j}+l_{i,j+1})-\frac{2}{v_{0}}\left(\frac{1}{c_{i,j}}+\frac{1}{c_{i,j+1}}\right)$$

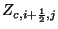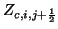The positivity requirements on $Z_{c,i+\frac{1}{2},j}$ and $Z_{c,i, j+\frac{1}{2}}$ force us to choose

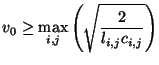$$v_{0}\geq \max_{i,j}\left(\sqrt{\frac{2}{l_{i,j}c_{i,j}}}\right)$$ (4.75)

Thus we have a simple CFL-type bound on the space step/time step ratio, which must be chosen greater than 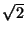$\sqrt{2}$ times the maximum value of the local group velocity 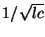$1/\sqrt{lc}$ over parallel junction locations 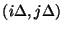$(i\Delta,j\Delta)$. The bound (4.63) converges to 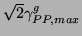$\sqrt{2}\gamma_{PP,max}^{g}$, as defined by (3.68), in the limit as the grid spacing $\Delta$ becomes small.