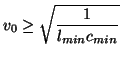Next: Comment: Passivity and Stability
Up: Varying Coefficients
Previous: Type II: Current-centered Network
Suppose we set all the impedances which connect one grid point to another to be equal to some constant 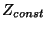 which is independent of position. Thus
which is independent of position. Thus
We then choose, to satisfy (4.33) and (4.34),
and this leads to the conditions
where
The lower bounds on 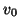 coincide when
coincide when
in which case we have
Since in general,
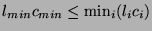 , for
, for 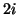 either even or odd, we are no longer at the optimal bound, and are forced to use a smaller time step than in the previous two cases, if we wish the network to remain concretely passive. This arrangement bears a strong resemblance to the MDWD network in [107] and [131], and discussed in §3.7. We will explore this similarity in more detail in §4.10. Many other choices are of the waveguide immittances satisfying (4.33) and (4.34) are of course possible.
either even or odd, we are no longer at the optimal bound, and are forced to use a smaller time step than in the previous two cases, if we wish the network to remain concretely passive. This arrangement bears a strong resemblance to the MDWD network in [107] and [131], and discussed in §3.7. We will explore this similarity in more detail in §4.10. Many other choices are of the waveguide immittances satisfying (4.33) and (4.34) are of course possible.



Next: Comment: Passivity and Stability
Up: Varying Coefficients
Previous: Type II: Current-centered Network
Stefan Bilbao
2002-01-22
![]() which is independent of position. Thus
which is independent of position. Thus