




Next: Boundary Conditions
Up: Definition
Previous: Phase and Group Velocity
Contents
Index
Energy Analysis
The frequency domain analysis above was applied to the case of the wave equation defined over an infinite domain
 , and thus boundary conditions have not been taken into account. Another way of examining the behaviour of the wave equation is similar to that which was discussed in Section 3.1.2, with regard to the oscillator, through the use of energetic techniques. Besides the fact that it may be applied to systems which are not linear and shift invariant, energy analysis also provides extremely useful insights regarding correct boundary termination, as well as important bounds on solution growth.
, and thus boundary conditions have not been taken into account. Another way of examining the behaviour of the wave equation is similar to that which was discussed in Section 3.1.2, with regard to the oscillator, through the use of energetic techniques. Besides the fact that it may be applied to systems which are not linear and shift invariant, energy analysis also provides extremely useful insights regarding correct boundary termination, as well as important bounds on solution growth.
In the first instance, consider again the wave equation defined over the entire real line, i.e., for
 . Taking the inner product of (6.2) with
. Taking the inner product of (6.2) with 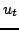 over
over
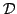 gives
gives
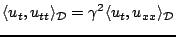 |
(6.13) |
and, employing integration by parts, one may arrive at
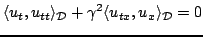 |
(6.14) |
Both of the terms in the above equation may be written as total derivatives with respect to time, i.e.,
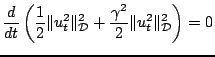 |
(6.15) |
or, more simply,
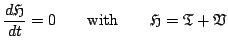 |
(6.16) |
and
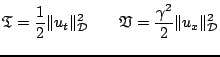 |
(6.17) |
Equation (6.16), and the non-negativity of the terms
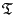 and
and
 above imply that
above imply that
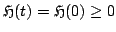 |
(6.18) |
Clearly, the non-negativity of
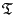 and
and
 also imply that
also imply that
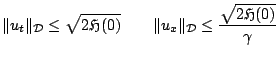 |
(6.19) |





Next: Boundary Conditions
Up: Definition
Previous: Phase and Group Velocity
Contents
Index
Stefan Bilbao
2006-11-15
![]() . Taking the inner product of (6.2) with
. Taking the inner product of (6.2) with ![]() over
over
![]() gives
gives
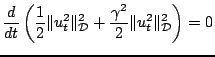
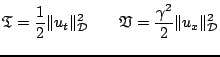
![]() and
and
![]() also imply that
also imply that