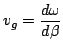Phase and Group Velocity

For a linear and shift-invariant 1D system such as the wave equation, with a dispersion relation 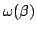$\omega(\beta)$, the phase velocity is defined by

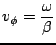$$v_{\phi} = \frac{\omega}{\beta}$$ (6.10)

The group velocity is defined by

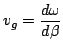$$v_{g} = \frac{d\omega}{d\beta}$$ (6.11)

In general, for a given system, the phase velocity describes the speed of propagation of a single component of the solution, and the group velocity the gross speed of disturbances. For hyperbolic systems, such as the wave equation, it must be true that the group velocity is bounded from above (i.e., there is a maximum speed at which disturbances may propagate), though this is not necessarily true of the phase velocity--the case of Timoshenko beam theory is an interesting example of this [100]. Most systems that will be examined in this book will be of hyperbolic type, with the exception of thin beams and plates, which do in fact allow infinite group velocities. Such anomalous behaviour is in general a result of simplifying assumptions, and disappears when more accurate models are employed.

In the case of the wave equation above, the phase velocity and group velocity are both constant, i.e.,

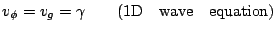$$v_{\phi}=v_{g}=\gamma\qquad{\rm (1D\quad wave\quad equation)}$$ (6.12)

In particular, the phase and group velocities are independent of frequency 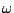$\omega$. Thus any wave-like solution to the 1D wave equation travels at a constant speed. One might surmise, using arguments from Fourier theory, that if all components of a solution travel at the same speed, then any possible solution must travel with this speed--this is, in fact, true, and is another means of arriving at the so-called traveling wave solution to the wave equation, to be discussed in §6.1.9.