Characteristics and Travelling Wave Solutions

As is well-known, the 1D wave equation possesses travelling-wave solutions. This should be readily apparent from an examination of the behaviour of the single plane wave solution defined in () of the form

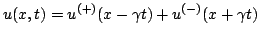$$u(x,t) = u^{(+)}(x-\gamma t)+u^{(-)}(x+\gamma t)$$ (6.32)

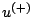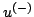for arbitrary functions $u^{(+)}$ and $u^{(-)}$, which represent rightward and leftward travelling waves of spatially non-dimensionalized speed 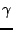$\gamma$, respectively. This decomposition, due to d'Alembert, may be arrived at directly in the time-space domain, through a change of variables, or through frequency domain analysis (see Problem ). Such a simple decomposition is peculiar to the 1D wave equation alone, and does not extend in general to more complex variants of the 1D wave equation (with some exceptions) or to the case of general wave equation in multiple dimensions. It is, however, the starting point for digital waveguide modelling, which is perhaps the best known of all physical modelling sound synthesis techniques, and will be discussed in more detail in Section 6.2.9.