




Next: Phase and Group Velocity
Up: Definition
Previous: Initial Conditions
Contents
Index
Frequency domain analysis is extremely revealing in the case of the wave equation in particular. Considering the case of a string defined over the spatial domain
 , a Fourier transform (in space) and a two-sided Laplace transform (in time) may be used. See Chapter 5 for more details. As a short-cut, one may analyze the behaviour of the test solution
, a Fourier transform (in space) and a two-sided Laplace transform (in time) may be used. See Chapter 5 for more details. As a short-cut, one may analyze the behaviour of the test solution
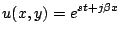 |
(6.6) |
where 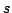 is interpreted as a complex frequency variable,
is interpreted as a complex frequency variable,
 , and
, and 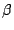 is a real wavenumber. It is easy to see that if
is a real wavenumber. It is easy to see that if
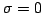 , such a test solution is, in fact a traveling wave of temporal frequency
, such a test solution is, in fact a traveling wave of temporal frequency
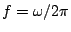 , and wavelength
, and wavelength
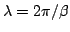 . Substituting such a solution into (6.2) gives
. Substituting such a solution into (6.2) gives
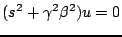 |
(6.7) |
Clearly the test solution 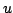 is non-zero everywhere, leading the characteristic equation
is non-zero everywhere, leading the characteristic equation
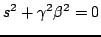 |
(6.8) |
which has roots
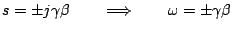 |
(6.9) |
This is known as the dispersion relation for the system (6.2); the frequency and wavenumber of a plane-wave solution are not independent. The fact that there are two solutions results from the fact that the wave equation is second order in time--the solutions correspond to left-going and right-going wave solutions.





Next: Phase and Group Velocity
Up: Definition
Previous: Initial Conditions
Contents
Index
Stefan Bilbao
2006-11-15
![]() , a Fourier transform (in space) and a two-sided Laplace transform (in time) may be used. See Chapter 5 for more details. As a short-cut, one may analyze the behaviour of the test solution
, a Fourier transform (in space) and a two-sided Laplace transform (in time) may be used. See Chapter 5 for more details. As a short-cut, one may analyze the behaviour of the test solution